题目内容

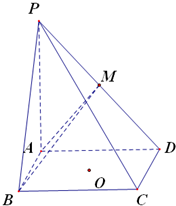
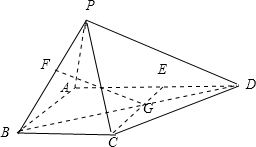
如图四棱锥P-ABCD中，ABCE为菱形，E、G、F分别是线段AD、CE、PB的中点．求证：FG∥平面PDC．
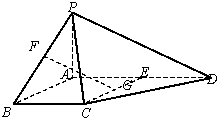
证明：连接BD与CE交于点0，∵E为AD的中点，ABCE为菱形，AE=BC=DE，
∴
CO
OD
=
BC
DE
=1，得到O为线段CE的中点，故O与点G重合．
∵
BG
GD
=
BC
ED
=1，∴G为BD的中点，又F为PB的中点，
∴FG∥PD，又∵FG?平面PDC，PD?平面PDC．
∴FG∥平面PDC．
练习册系列答案
相关题目
长方体ABCD-A1B1C1D1中，AB=3，AD=2，AA1=1，则从A点沿表面到C1点的最短距离为______．
如图，在四棱锥P-ABCD中，底面ABCD是正方形，PD⊥底面ABCD，E为侧棱PD的中点，AC与BD的交点为O．求证：
（1）直线OE∥平面PBC；
（2）平面ACE⊥平面PBD．
如图，梯形ABCD和正△PAB所在平面互相垂直，其中AB∥DC，AD=CD=
1
2
AB，且O为AB中点．
（I）求证：BC∥平面POD；
（II）求证：AC⊥PD．
如图，在四棱锥P-ABCD中，底面ABCD是矩形，O为底面中心，PA⊥平面ABCD，PA=AD=2AB．M是PD的中点
（1）求证：直线MO∥平面PAB；
（2）求证：平面PCD⊥平面ABM．
如图，直三棱柱ABC-A′B′C′，∠BAC=90°，AB=AC=
2
，AA′=1，点M，N分别为A′B和B′C′的中点．
（Ⅰ）证明：MN∥平面A′ACC′；
（Ⅱ）求三棱锥A′-MNC的体积．
（椎体体积公式V=
1
3
Sh，其中S为地面面积，h为高）
如图，四棱锥P-ABCD的底面ABCD是正方形，PA⊥底面ABCD，E，F分别是AC，PB的中点．
（Ⅰ）证明：EF∥平面PCD；
（Ⅱ）若PA=AB，求EF与平面PAC所成角的大小．
在斜三棱柱ABC-A1B1C1中，侧面ACC1A1⊥平面ABC，∠ACB=90°．
（1）求证：BC⊥AA1．
（2）若M，N是棱BC上的两个三等分点，求证：A1N∥平面AB1M．
在四棱锥P-ABCD中，底面ABCD为直角梯形，BC∥AD，∠ADC=90°，BC=CD=
1
2
AD，PA=PD，E，F为AD，PC的中点．
（Ⅰ）求证：PA∥平面BEF；
（Ⅱ）求证：AD⊥PB．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网