题目内容
9.已知椭圆$\frac{x^2}{4}+\frac{y^2}{a^2}=1$与双曲线$\frac{x^2}{a}-\frac{y^2}{2}=1$有相同的焦距,则实数a=1.分析 由题意可得a>0,即有焦点在x轴上,分别求得椭圆和双曲线的半焦距,解方程可得a=1.
解答 解:由题意可得a>0,即有焦点在x轴上,
可得椭圆$\frac{x^2}{4}+\frac{y^2}{a^2}=1$的半焦距为$\sqrt{4-{a}^{2}}$,
双曲线$\frac{x^2}{a}-\frac{y^2}{2}=1$的半焦距为$\sqrt{a+2}$,
由题意可得$\sqrt{4-{a}^{2}}$=$\sqrt{a+2}$,
解得a=1.
故答案为:1.
点评 本题考查椭圆和双曲线的方程和性质,考查焦点的位置判断和焦距的求法,属于基础题.

练习册系列答案
相关题目
 如图所示,在正方体ABCD-A1B1C1D1中,E、G、H分别是BC、C1D1、AA1、的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E、G、H分别是BC、C1D1、AA1、的中点.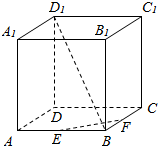 在正方体ABCD-A1B1C1D1中,E、F分别是AB,BC的中点,求异面直线BD1、EF所成角的大小.
在正方体ABCD-A1B1C1D1中,E、F分别是AB,BC的中点,求异面直线BD1、EF所成角的大小.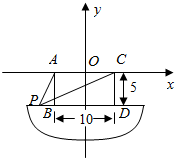 船上两根高5m的桅杆相距10m,一条30m长的绳子两端系在桅杆的顶上,并按如图所示的方式绷紧,假设绳子位于两根桅杆所在的平面内,求绳子与甲板接触点P到桅杆AB的距离.
船上两根高5m的桅杆相距10m,一条30m长的绳子两端系在桅杆的顶上,并按如图所示的方式绷紧,假设绳子位于两根桅杆所在的平面内,求绳子与甲板接触点P到桅杆AB的距离. 已知函数f(x)=$\left\{\begin{array}{l}{2^x},x<0\\ 2{(x-1)^2}-1,x≥0\end{array}\right.$.
已知函数f(x)=$\left\{\begin{array}{l}{2^x},x<0\\ 2{(x-1)^2}-1,x≥0\end{array}\right.$.