题目内容
8.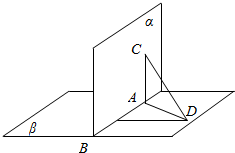 已知A,B,是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=12,AB=4,BD=3,求线段CD的长.
已知A,B,是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=12,AB=4,BD=3,求线段CD的长.
分析 由于本题中的二面角是直角,且两线段都与棱垂直,可根据题意作出相应的长方体,CD恰好是此长方体的体对角线,由长方体的性质求出其长度即可.
解答  解:如图,由于此题的二面角是直角,且线段AC,BD分别在α,β内垂直于棱l,AC=12,AB=4,BD=3,
解:如图,由于此题的二面角是直角,且线段AC,BD分别在α,β内垂直于棱l,AC=12,AB=4,BD=3,
作出以线段AB,BD,AC为棱的长方体,CD即为长方体的对角线,
由正方体的性质知,CD=$\sqrt{1{2}^{2}+{4}^{2}+{3}^{2}}$=13.
点评 本题考查与二面角有关的线段长度计算问题,根据本题的条件选择作出长方体,利用长方体的性质求线段的长度,大大简化了计算,具体解题中要注意此类问题的合理转化.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
13.定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有(x2-x1)[f(x2)-f(x1)]<0.则( )
| A. | f(1)<f(-2)<f(3) | B. | f(3)<f(1)<f(-2) | C. | f(一2)<f(1)<f(3) | D. | f(3)<f(-2)<f(1) |
 如图所示,在正方体ABCD-A1B1C1D1中,E、G、H分别是BC、C1D1、AA1、的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E、G、H分别是BC、C1D1、AA1、的中点. 已知函数f(x)=$\left\{\begin{array}{l}{2^x},x<0\\ 2{(x-1)^2}-1,x≥0\end{array}\right.$.
已知函数f(x)=$\left\{\begin{array}{l}{2^x},x<0\\ 2{(x-1)^2}-1,x≥0\end{array}\right.$.