题目内容
6.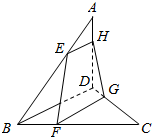 如图所示,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD,DA上的点.且满足$\frac{AE}{EB}$=$\frac{AH}{HD}$=$\frac{1}{2}$,$\frac{CF}{FB}$=$\frac{CG}{GD}$=2.
如图所示,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD,DA上的点.且满足$\frac{AE}{EB}$=$\frac{AH}{HD}$=$\frac{1}{2}$,$\frac{CF}{FB}$=$\frac{CG}{GD}$=2.(1)求证:四边形EFGH是梯形;
(2)若BD=a.求梯形EFGH的中位线的长.
分析 (1)利用比例关系,求出EH∥BD,FG∥BD,EH=$\frac{1}{3}BD$,FG=$\frac{2}{3}$BD,即可证明四边形EFGH是梯形;
(2)EH=$\frac{1}{3}BD$=$\frac{1}{3}a$,FG=$\frac{2}{3}$BD=$\frac{2}{3}$a,即可求梯形EFGH的中位线的长.
解答 (1)证明:∵$\frac{AE}{EB}$=$\frac{AH}{HD}$=$\frac{1}{2}$,$\frac{CF}{FB}$=$\frac{CG}{GD}$=2,∴EH∥BD,FG∥BD,EH=$\frac{1}{3}BD$,FG=$\frac{2}{3}$BD.
∴EH∥FG,EH≠FG,
∴四边形EFGH是梯形;
(2)解:∵BD=a,
∴EH=$\frac{1}{3}BD$=$\frac{1}{3}a$,FG=$\frac{2}{3}$BD=$\frac{2}{3}$a,
∴梯形EFGH的中位线的长为$\frac{a}{2}$.
点评 本题考查直线与直线平行的判定,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
15.等差数列{an}中an>0,且a1+a2+…+a10=30,则a5+a6=( )
| A. | 3 | B. | 6 | C. | 9 | D. | 36 |
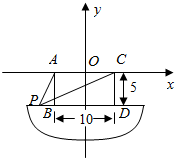 船上两根高5m的桅杆相距10m,一条30m长的绳子两端系在桅杆的顶上,并按如图所示的方式绷紧,假设绳子位于两根桅杆所在的平面内,求绳子与甲板接触点P到桅杆AB的距离.
船上两根高5m的桅杆相距10m,一条30m长的绳子两端系在桅杆的顶上,并按如图所示的方式绷紧,假设绳子位于两根桅杆所在的平面内,求绳子与甲板接触点P到桅杆AB的距离. 已知函数f(x)=$\left\{\begin{array}{l}{2^x},x<0\\ 2{(x-1)^2}-1,x≥0\end{array}\right.$.
已知函数f(x)=$\left\{\begin{array}{l}{2^x},x<0\\ 2{(x-1)^2}-1,x≥0\end{array}\right.$.