题目内容
(本题满分14分)
顶点在坐标原点,开口向上的抛物线经过点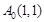 ,过点
,过点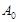 作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点
作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点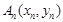 作抛物线的切线交x轴于点
作抛物线的切线交x轴于点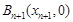 .
.
(I)求数列{ xn },{ yn}的通项公式 ;
;
(II)设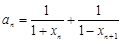 ,数列{ an}的前n项和为Tn.求证:
,数列{ an}的前n项和为Tn.求证: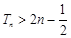 ;
;
(III)设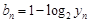 ,若对于任意正整数n,不等式
,若对于任意正整数n,不等式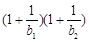 …
…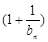 ≥
≥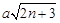 成立,求正数a的取值范围.
成立,求正数a的取值范围.
顶点在坐标原点,开口向上的抛物线经过点
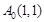 ,过点
,过点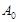 作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点
作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点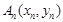 作抛物线的切线交x轴于点
作抛物线的切线交x轴于点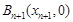 .
.(I)求数列{ xn },{ yn}的通项公式
 ;
;(II)设
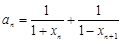 ,数列{ an}的前n项和为Tn.求证:
,数列{ an}的前n项和为Tn.求证: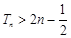 ;
;(III)设
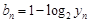 ,若对于任意正整数n,不等式
,若对于任意正整数n,不等式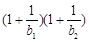 …
…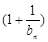 ≥
≥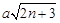 成立,求正数a的取值范围.
成立,求正数a的取值范围.(I)由已知得抛物线方程为
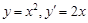 . ………………………………………2分
. ………………………………………2分则设过点
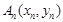 的切线为
的切线为 .
.令
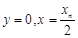 ,故
,故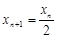 .
.又
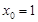 ,所以
,所以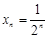 ,
,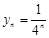 . ……………………………………………4分
. ……………………………………………4分(II)由(1)知
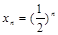 .
.所以
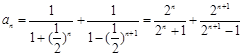
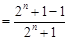 +
+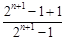
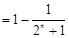 +1+
+1+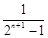
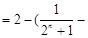
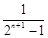 ) .……………………………………………6分
) .……………………………………………6分由
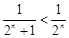 ,
,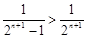 ,
,得
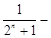
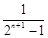
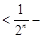
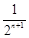 .
.所以
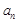
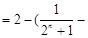
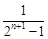 )
)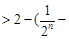
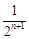 ).…………………………7分
).…………………………7分从而
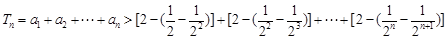
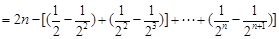
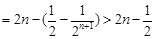 ,
,即
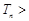
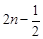 .…………………………………………………………………9分
.…………………………………………………………………9分(III)由于
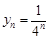 ,故
,故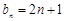 .
.对任意正整数n,不等式
 成立,
成立,即
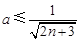
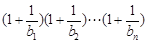 恒成立.
恒成立.设
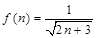
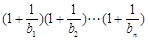 ,………………………………10分
,………………………………10分则
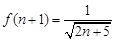
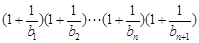 .
.故
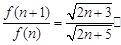
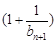 =
=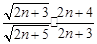 =
=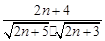
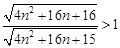
所以
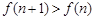 ,故
,故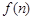 递增.…………………………………………12分
递增.…………………………………………12分则
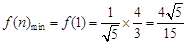 .
.故
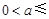
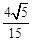 .…………………………………………………………………14分
.…………………………………………………………………14分略

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
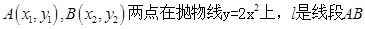 的垂直平分线.
的垂直平分线.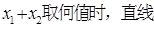
 ?
? 轴上截距的取值范围.
轴上截距的取值范围. 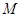 到点
到点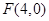 的距离比它到定直线
的距离比它到定直线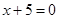 的距离小1,则点
的距离小1,则点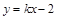 交抛物线
交抛物线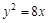 于A,B两点,若AB中点的横坐标是2,则
于A,B两点,若AB中点的横坐标是2,则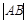 =______
=______ 与抛物线
与抛物线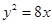 只有一个公共点的直线有 ( )
只有一个公共点的直线有 ( )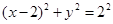 的圆心恰是抛物线的焦点,
的圆心恰是抛物线的焦点,
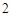 ,且过抛物线焦点,它依次截抛物线和圆于
,且过抛物线焦点,它依次截抛物线和圆于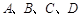 四点,求
四点,求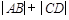 的值.
的值. 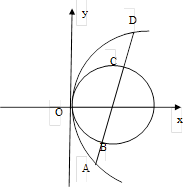
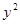 = 2x上的动点,过点P作y轴垂线PM,垂足为M, 点A的坐标是
= 2x上的动点,过点P作y轴垂线PM,垂足为M, 点A的坐标是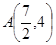 ,则| PA | + | PM |的最小值是
,则| PA | + | PM |的最小值是 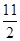
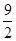
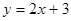 与抛物线
与抛物线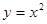 所围成的图形面积是
所围成的图形面积是