题目内容
【题目】已知抛物线y2=4 ![]() x的焦点为F,A、B为抛物线上两点,若
x的焦点为F,A、B为抛物线上两点,若 ![]() =3
=3 ![]() ,O为坐标原点,则△AOB的面积为( )
,O为坐标原点,则△AOB的面积为( )
A.8 ![]()
B.4 ![]()
C.2 ![]()
D.![]()
【答案】B
【解析】解:抛物线y2=4 ![]() x的焦点为F(
x的焦点为F( ![]() ,0),由抛物线的定义可知:|AF|=|AD|,|BC|=|BF|,
,0),由抛物线的定义可知:|AF|=|AD|,|BC|=|BF|,
过B做BE⊥AD,
由 ![]() =3
=3 ![]() ,则丨
,则丨 ![]() 丨=丨
丨=丨 ![]() 丨,
丨,
∴|AB|=2|AE|,由抛物线的对称性,不妨设直线的斜率为正,
∴直线AB的倾斜角为60°,直线AB的方程为y= ![]() (x﹣
(x﹣ ![]() )=
)= ![]() x﹣3,
x﹣3,
联立直线AB与抛物线的方程可得: ![]() ,整理得:3x2﹣10
,整理得:3x2﹣10 ![]() x+9=0,
x+9=0,
由韦达定理可知:x1+x2= ![]() ,则丨AB丨=x1+x2+p=
,则丨AB丨=x1+x2+p= ![]() +2
+2 ![]() =
= ![]() ,
,
而原点到直线AB的距离为d= ![]() =
= ![]() ,
,
则三角形△AOB的面积S= ![]() 丨AB丨d=
丨AB丨d= ![]()
![]()
![]() =4
=4 ![]() ,
,
∴当直线AB的倾斜角为120°时,同理可求S=4 ![]() ,
,
故选B.
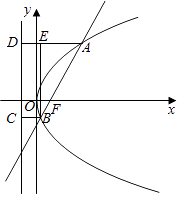
根据抛物线的定义,不难求出,|AB|=2|AE|,由抛物线的对称性,不妨设直线的斜率为正,所以直线AB的倾斜角为60°,可得直线AB的方程,与抛物线的方程联立,求出A,B的坐标,即可求出△AOB的面积.

【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算:电费每月用电不超过100度时,按每度0.57元计算;每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.
(Ⅰ)设月用电![]() 度时,应交电费
度时,应交电费![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)小明家第一季度缴纳电费情况如下:
月份 | 一月 | 二月 | 三月 | 合计 |
交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用电多少度?
【题目】某市春节7家超市的广告费支出x(万元)和销售额y(万元)数据如下,
超市 | A | B | C | D | E | F | G |
广告费支出x | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额y | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)请根据上表提供的数据.用最小二乘法求出y关于x的线性回归方程; ![]() =
= ![]() x+
x+ ![]()
(2)用二次函数回归模型拟合y与x的关系,可得回归方程: ![]() =﹣0.17x2+5x+20. 经计算二次函数回归模型和线性回归模型的R2分别约为0.93和0.75,请用R2说明选择哪个回归模型更合适.并用此模型预测A超市广告费支出为3万元时的销售额,
=﹣0.17x2+5x+20. 经计算二次函数回归模型和线性回归模型的R2分别约为0.93和0.75,请用R2说明选择哪个回归模型更合适.并用此模型预测A超市广告费支出为3万元时的销售额,
参考数据及公式: ![]() =8,
=8, ![]() =42.
=42. ![]() xiyi=2794,
xiyi=2794, ![]() x
x ![]() =708,
=708,![]() =
= 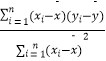 =
= 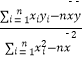 ,
, ![]() =
= ![]() ﹣
﹣ ![]() x.
x.