题目内容
【题目】已知数列{an}的首项a1=1，且an+1= 
（n∈N*）．
（1）证明：数列{ 
}是等差数列，并求数列{an}的通项公式；
（2）设bn=anan+1 ， 求数列{bn}的前n项和Tn ．
【答案】
（1）证明：由an+1= 
（n∈N*），两边取倒数可得： 
﹣ 
=2．
∴数列{ }是等差数列，公差为2，首项为1．
∴ =1=2（n﹣1）=2n﹣1．
∴an= 
．
（2）解：bn=anan+1= 
= 
．
∴数列{bn}的前n项和Tn= 
+…+ 
= 
= 
．
【解析】（1）由an+1= 
（n∈N*），两边取倒数可得： 
﹣ 
=2．即可证明．（2）bn=anan+1= 
= 
．利用裂项求和方法即可得出．
【考点精析】根据题目的已知条件，利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案，需要掌握数列{an}的前n项和sn与通项an的关系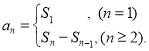
；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】某地西红柿从
月
日起开始上市．通过市场调查，得到西红柿种植成本
(就是每
公斤西红柿的种植成本，单位：元)与上市时间
(单位：天)的数据如下表：
上市时间 | 50 | 110 | 250 |
种植成本 | 150 | 108 | 150 |
(1)根据上表数据，从下列函数中选取一个函数描述西红柿种植成本与上市时间的变化关系：
；
；
；
，并求出函数解析式；
(2)利用你选取的函数，求西红柿种植成本最低时的上市天数及最低种植成本．
【题目】濮阳市黄河滩区某村2010年至2016年人均纯收入（单位：万元）的数据如下表：
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
（Ⅰ）求y关于x的线性回归方程；
（Ⅱ）利用（Ⅰ）中的回归方程，分析2010年至2016年该村人均纯收入的变化情况，并预测该村2017年人均纯收入．
附：回归直线的斜率和截距的最小乘法估计公式分别为： 
= 
， 
= 
﹣ 
．
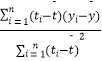