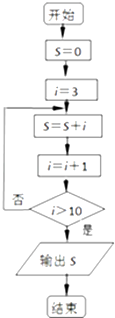
题目内容
【题目】如图,在底面是菱形的四棱锥P—ABCD中,∠ABC=60°,PA=AC=a,PB=PD= ![]() ,点E是PD的中点.
,点E是PD的中点.
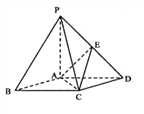
(Ⅰ)求证:PA⊥平面ABCD;
(Ⅱ)求二面角E—AC—D的大小;
(Ⅲ)求点P到平面EAC的距离.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(I)证明PA⊥AB,PA⊥AD,AB、AD是平面ABCD内的两条相交直线,即可证明PA⊥平面ABCD;(Ⅱ)如图,建立空间直角坐标系A—xyz, 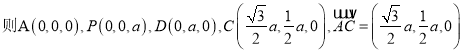 ,
,![]() 求出平面EAC的法向量为
求出平面EAC的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,
, ![]() 即得二面角大小(Ⅲ)由(II)问得,点P平面EAC的距离
即得二面角大小(Ⅲ)由(II)问得,点P平面EAC的距离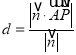 代入计算即得解.
代入计算即得解.
试题解析:
(Ⅰ)证明:因为底面ABCD是菱形,∠ABC=60°
所以AB=AD=AC=a,
在△PAB中,可证PA2+AB2=2a2 = PB2 ∴PA⊥AB.
同理,PA⊥AD,所以PA⊥平面ABCD.
(II)如图,建立空间直角坐标系A—xyz

![]()
设平面EAC的法向量为![]() ,
, ![]() ,
, ![]() ,又平面ACD的法向量为
,又平面ACD的法向量为![]()
![]() ,即二面角E—AC—D的大小为
,即二面角E—AC—D的大小为![]() ;
;
(III)点P平面EAC的距离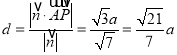 。
。

【题目】濮阳市黄河滩区某村2010年至2016年人均纯收入(单位:万元)的数据如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求y关于x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2010年至2016年该村人均纯收入的变化情况,并预测该村2017年人均纯收入.
附:回归直线的斜率和截距的最小乘法估计公式分别为: ![]() =
= 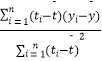 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
【题目】某农场共有土地50亩,这些地可种西瓜、棉花、玉米.这些农作物每亩地所需劳力和预计产值如下表.若该农场有20名劳动力,应怎样计划才能使每亩地都能种上作物(玉米必种),所有劳动力都被安排工作(每名劳动力只能种植一种作物)且作物预计总产值达最高?
作物 | 劳力/亩 | 产值/亩 |
西瓜 | 1/2 | 0.6万元 |
棉花 | 1/3 | 0.5万元 |
玉米 | 1/4 | 0.3万元 |