题目内容
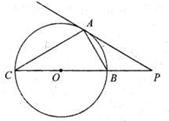
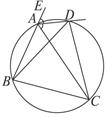
如图,四边形 是圆内接四边形,延长
是圆内接四边形,延长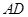 与的延长线
与的延长线 交于点
交于点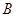 ,且
,且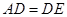 ,
, 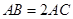 .
.

(1)求证: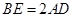 ;
;
(2)当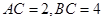 时,求
时,求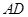 的长.
的长.
 是圆内接四边形,延长
是圆内接四边形,延长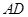 与的延长线
与的延长线 交于点
交于点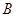 ,且
,且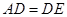 ,
, 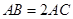 .
.
(1)求证:
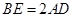 ;
;(2)当
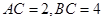 时,求
时,求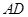 的长.
的长.(Ⅰ) 证明 ∽
∽ ,则
,则 .由
.由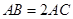 ,所以
,所以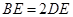 . (4分)
. (4分)
结合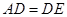 ,得到
,得到
(Ⅱ) .
.
 ∽
∽ ,则
,则 .由
.由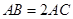 ,所以
,所以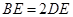 . (4分)
. (4分)结合
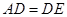 ,得到
,得到
(Ⅱ)
 .
. 试题分析:(Ⅰ) 因为四边形
 为圆的内接四边形,所以
为圆的内接四边形,所以 (1分)
(1分)又
 所以
所以 ∽
∽ ,则
,则 . (3分)
. (3分)而
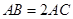 ,所以
,所以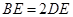 . (4分)
. (4分)又
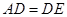 ,从而
,从而 (5分)
(5分)(Ⅱ)由条件得
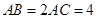 . (6分)
. (6分)设
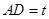 ,根据割线定理得
,根据割线定理得 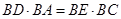 ,即
,即
所以
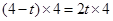 ,解得
,解得  ,即
,即 . (10分)
. (10分)点评:中档题,选考内容,难度一般不大。处理圆中的问题时,要注意挖掘相等的角,发现三角形的全等或相似关系。

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
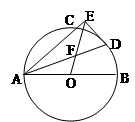
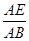 =
=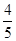 ,求
,求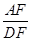 的值.
的值.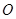 的半径为3,两条弦
的半径为3,两条弦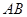 ,
,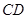 交于点
交于点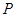 ,且
,且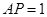 ,
, 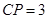 ,
,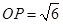 .
.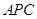 ≌△
≌△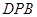 .
.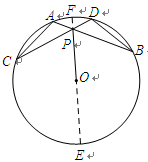
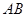 是圆
是圆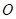 的直径,
的直径,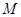 为圆上一点,
为圆上一点,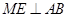 ,垂足为
,垂足为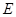 ,点
,点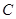 为圆
为圆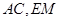 交于点
交于点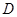 ,
,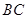 交
交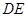 于点
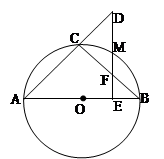
于点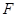 .
.
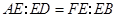 ;(2)
;(2)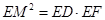 .
.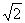 ,
,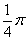 ),曲线C的参数方程为
),曲线C的参数方程为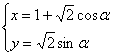 (
(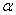 为参数),则点M到曲线C上的点的距离的最小值为 .
为参数),则点M到曲线C上的点的距离的最小值为 .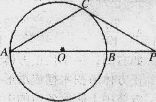
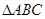 的面积为1,点
的面积为1,点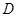 在
在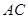 上,
上,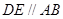 ,连结
,连结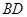 ,设
,设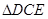 、
、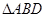 、
、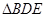 中面积最大者的值为
中面积最大者的值为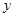 ,则
,则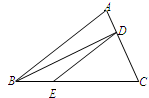
 ,则
,则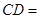
 为锐角△
为锐角△ 的内心,且
的内心,且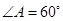 ,点
,点 为内切圆
为内切圆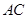 的切点,过点
的切点,过点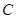 作直线
作直线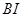 的垂线,垂足为
的垂线,垂足为 .
.
 ;
; 的值.
的值.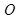 的切线,A为切点,割线PBC过圆心O,PA=10,PB=5,则AC长为
的切线,A为切点,割线PBC过圆心O,PA=10,PB=5,则AC长为