题目内容
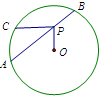
已知 的面积为1,点
的面积为1,点 在
在 上,
上,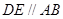 ,连结
,连结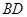 ,设
,设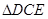 、
、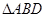 、
、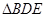 中面积最大者的值为
中面积最大者的值为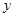 ,则
,则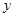 的最小值为 .
的最小值为 .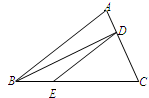
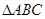 的面积为1,点
的面积为1,点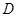 在
在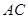 上,
上,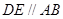 ,连结
,连结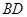 ,设
,设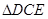 、
、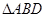 、
、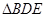 中面积最大者的值为
中面积最大者的值为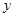 ,则
,则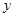 的最小值为 .
的最小值为 .
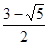
试题分析:解:设CD:CA=k,则因为点D在AC上,所以0<k<1 ,∵DE∥AB,∴△DCE∽△ACB,∴S△DCE:S△ACB=(CD:CA)2=k2,∵S△ABC=1,∴S△DCE=k2; ,∵AD:AC=(AC-CD):AC=1-k,∴S△ABD:S△ABC=AD:AC=1-k,∴S△ABD=1-k,∵DE∥AB,∴CE:BE=CD:AD=k:(1-k) ,∵S△DCE:S△BDE=CE:BE=k:(1-k)∴S△BDE=[(1-k):k]×S△DCE=-k2+k,当k2=1-k时,k2+k-1=0,∴k=
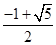 ;当k2=-k2+k时,2k2-k=0,∴k=
;当k2=-k2+k时,2k2-k=0,∴k=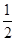 当1-k=-k2+k时,k2-2k+1=0,∴k=1,故可知y=1-k,0<k≤
当1-k=-k2+k时,k2-2k+1=0,∴k=1,故可知y=1-k,0<k≤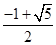 k2,
k2,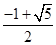 <k<1,故可知当k=
<k<1,故可知当k=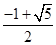 时,y有最小值
时,y有最小值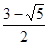
点评:本题考查三角形面积的计算,考查函数的最值,考查分段函数,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
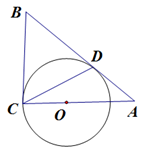
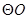 ,且AB是的
,且AB是的
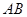 、
、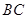 分别与圆
分别与圆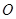 相切于
相切于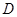 、
、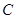 ,
,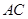 经过圆心
经过圆心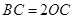 ,求证:
,求证: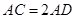 .
.
 的外接圆,直线
的外接圆,直线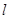 为⊙O的切线,切点为
为⊙O的切线,切点为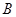 ,直线
,直线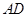 ∥
∥ 于
于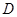 ,交⊙O于
,交⊙O于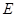 ,
,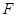 为
为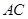 上一点,且
上一点,且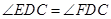 .
.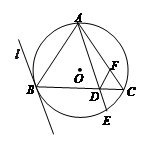
 ;
; 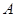 、
、 是圆内接四边形,延长
是圆内接四边形,延长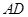 与的延长线
与的延长线 交于点
交于点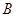 ,且
,且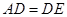 ,
, 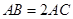 .
.
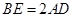 ;
;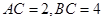 时,求
时,求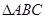 的三个顶点都在⊙O上,
的三个顶点都在⊙O上,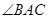 的平分线与BC边和⊙O分别交于点D、E.
的平分线与BC边和⊙O分别交于点D、E.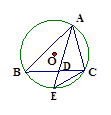
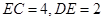 ,求
,求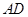 的长.
的长.
 ;
;
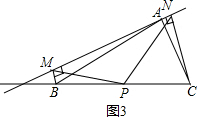
 是⊙
是⊙ 的一条弦,点
的一条弦,点 为
为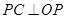 ,
,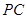 交⊙
交⊙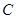 ,若
,若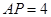 ,
,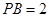 ,则
,则