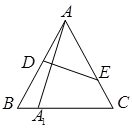题目内容
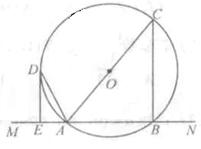
如图,⊙ 的半径为3,两条弦
的半径为3,两条弦 ,
, 交于点
交于点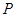 ,且
,且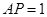 ,
, 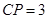 ,
,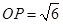 .
.
求证:△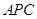 ≌△
≌△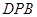 .
.
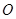 的半径为3,两条弦
的半径为3,两条弦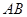 ,
,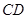 交于点
交于点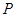 ,且
,且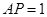 ,
, 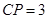 ,
,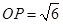 .
.求证:△
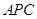 ≌△
≌△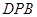 .
.
利用相交弦定理来和相似三角形的性质加以证明即可。
试题分析:证明:延长
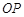 交⊙
交⊙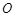 与点
与点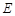 ,
,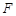 , 2分
, 2分由相交弦定理得
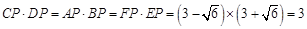 , 6分
, 6分又
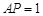 ,
,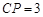 ,
,故
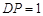 ,
,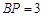 , 8分
, 8分所以
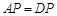 ,
,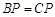 ,
,而
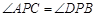 ,
,所以△
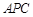 ≌△
≌△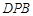 . 10分
. 10分点评:主要是考查了全等三角形的证明的运用,属于基础题。

练习册系列答案
相关题目
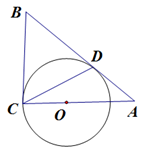
 是圆的内接四边形,
是圆的内接四边形,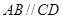 ,过
,过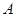 点的圆的切线与
点的圆的切线与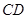 的延长线交于
的延长线交于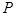 点,证明:
点,证明: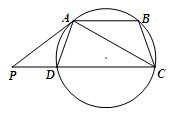
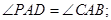
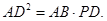
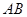 、
、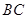 分别与圆
分别与圆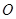 相切于
相切于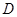 、
、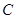 ,
,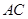 经过圆心
经过圆心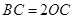 ,求证:
,求证: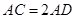 .
.
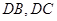 是⊙
是⊙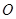 的两条切线,
的两条切线,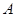 是圆上一点,已知
是圆上一点,已知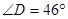 ,则
,则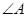 = .
= .
 交圆
交圆 于
于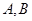 两点,
两点,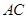 是直径,
是直径,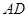 平分
平分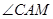 ,交圆
,交圆 , 过
, 过 丄
丄 .
.
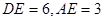 ,求
,求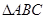 的面积
的面积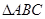 中,
中,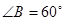 ,
,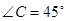 ,高
,高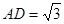 ,在
,在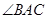 内作射线
内作射线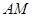 交
交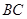 于点
于点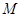 ,则
,则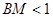 的概率为( )
的概率为( )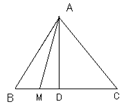
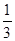
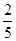
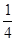
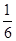
 是圆内接四边形,延长
是圆内接四边形,延长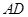 与的延长线
与的延长线 交于点
交于点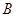 ,且
,且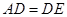 ,
, 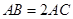 .
.
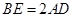 ;
;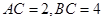 时,求
时,求