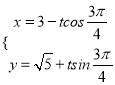题目内容
【题目】已知平面α和β，在平面α内任取一条直线a，在β内总存在直线b∥a，则α与β的位置关系是____(填“平行”或“相交”).
【答案】平行
【解析】假设
,则在平面
内,与
相交的直线
,设
,对
内的任意直线
,若
过点A,则a与b相交, 若
不过点A,则a与b异面,即
内不存在直线b//a,这与在平面
内任取一条直线a,在
内总存在直线b//a矛盾,故假设不成立, α与β的位置关系是平行,故填平行.
点睛:本题应用反证法证明结论成立. 假设原命题不成立，经过正确的推理，最后得出矛盾，因此说明假设不成立，从而证明了原命题成立，这样的证明方法叫做反证法．用反证法证明命题时要注意以下两点：①反证法必须以否定结论进行推理，即应把结论的反面作为条件，进行推证，否则就不是反证法．②反证法的关键是在正确的推理下得出矛盾．这个矛盾可以与已知条件矛盾，或与假设矛盾，或与定义、公理、定理、事实矛盾等．
练习册系列答案
相关题目
