题目内容
【题目】已知椭圆G:![]() ,过点A(0,5),B(﹣8,﹣3),C、D在该椭圆上,直线CD过原点O,且在线段AB的右下侧.
,过点A(0,5),B(﹣8,﹣3),C、D在该椭圆上,直线CD过原点O,且在线段AB的右下侧.
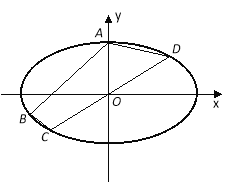
(1)求椭圆G的方程;
(2)求四边形ABCD 的面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题分析:(1)先将点A(0,5),B(-8,3),代入椭圆的方程解得:a=10 b=5,最后写出椭圆G的方程;(2)连OB,则四边形ABCD的面积![]() ,
,![]() 分别表示A,B到直线CD的距离,设CD:-kx+y=0,代入椭圆方程消去y得到关于x的一元二次方程,再结合求根公式即可求得四边形ABCD的面积,最后结合基本不等式求最大值,从而解决问题
分别表示A,B到直线CD的距离,设CD:-kx+y=0,代入椭圆方程消去y得到关于x的一元二次方程,再结合求根公式即可求得四边形ABCD的面积,最后结合基本不等式求最大值,从而解决问题
试题解析:(1)将点A(0,5),B(﹣8,﹣3)代入椭圆G 的方程解得:
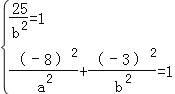 ,解得:a2=100,b2=25.
,解得:a2=100,b2=25.
∴椭圆G的方程为:![]() ;
;
(2)连结OB,
则![]() ,---7分
,---7分
其中dA,dB分别表示点A,点B 到直线CD 的距离.
设直线CD方程为y =kx,代入椭圆方程![]() ,得x2+4k2x2﹣100=0,
,得x2+4k2x2﹣100=0,
解得:![]() ,
,
∴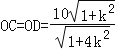 ,
,
又![]() ,
,![]() ,
,
则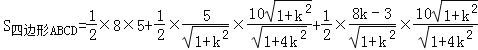
=![]() .
.
当且仅当k=1时 取等号。

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目