题目内容
【题目】某地区2008年至2014年农村居民家庭纯收入y（单位：千元）的数据如下表：
年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2．9 | 3．3 | 3．6 | 4．4 | 4．8 | 5．2 | 5．9 |
（Ⅰ）求y关于
的线性回归方程；
（Ⅱ）利用（Ⅰ）中的回归方程，分析2008年至2014年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2016年农村居民家庭人均纯收入．
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
，
．
【答案】（Ⅰ）
；（Ⅱ）6．8千元．
【解析】
试题分析：（Ⅰ）根据回归直线的斜率和截距的最小二乘法估计公式，即可求得回归直线方程为；（Ⅱ）因为回归直线的斜率
，故2008年至2014年该地区农村居民家庭人均纯收入逐年递增，平均每年增加0．5千元，因为2008年对应的为x=1,以此类推，2016年为x=9，所以预测该地区2016年农村居民家庭人均纯收入只需将x=9代入即可
试题解析：（Ⅰ）由所给数据得，
，
，
，
，
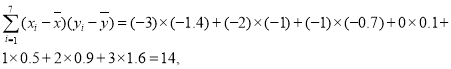
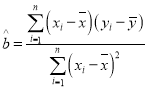
所求的回归直线方程为．
（Ⅱ）由（Ⅰ）知，，故2008年至2014年该地区农村居民家庭人均纯收入逐年递增，平均每年增加0．5千元．
将2016年的年份代换
代人回归直线方程，得
，
故预测该地区2016年农村居民家庭人均纯收入为6．8千元．
练习册系列答案
相关题目
