题目内容
2.已知函数f(x)=lnx-a(x-1),其中a>0.(1)若函数f(x)在(0,+∞)上有极大值0,求a的值;
(2)讨论并求出函数f(x)在区间[$\frac{1}{e}$,e]上的最大值.
分析 (1)求f(x)的导数,讨论导数的正负,可得f(x)的单调区间,利用函数f(x)在(0,+∞)上有极大值0,即可求a的值;
(2)分类讨论,利用函数的单调性,结合函数的定义域,求出函数f(x)在区间[$\frac{1}{e}$,e]上的最大值.
解答 解:(1)f(x)定义域为(0,+∞),
求导数,得f′(x)=$\frac{1-ax}{x}$
当0<x<$\frac{1}{a}$时,f′(x)>0;当x>$\frac{1}{a}$时,f′(x)<0,
∴f(x)的单调增区间为(0,$\frac{1}{a}$),f(x)的单调减区间为($\frac{1}{a}$,+∞)
因此,f(x)的极大值为f($\frac{1}{a}$)=-lna-1+a
∵-lna-1+a=0
∴a=1;
(2)由(1)知,f(x)的单调增区间为(0,$\frac{1}{a}$),f(x)的单调减区间为($\frac{1}{a}$,+∞),
∴e<$\frac{1}{a}$,即0<a<$\frac{1}{e}$,函数在区间[$\frac{1}{e}$,e]上单调递增,∴x=e时,f(x)max=lne-a(e-1);
$\frac{1}{e}$≤$\frac{1}{a}$≤e,即$\frac{1}{e}$≤a≤e,函数在区间[$\frac{1}{e}$,$\frac{1}{a}$]上单调递增,在[$\frac{1}{a}$,e]上单调递减,
∴x=$\frac{1}{a}$时,f(x)max=-lna-1+a;
e>$\frac{1}{a}$,即a>$\frac{1}{e}$,函数在区间[$\frac{1}{e}$,e]上单调递减,∴x=$\frac{1}{e}$时,f(x)max=-1-a($\frac{1}{e}$-1).
点评 本题考查导数知识的综合运用,考查函数的单调性与极大值,考查分类讨论的数学思想,属于中档题.

| A. | $\frac{π}{6}≤θ≤\frac{π}{2}$ | B. | $\frac{π}{3}≤θ≤\frac{π}{2}$ | C. | $0≤θ≤\frac{π}{3}$ | D. | $0<θ<\frac{2π}{3}$ |
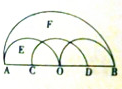 如图在以OA为半径的半圆M中,有三个半径为1的相同的半圆,在半圆M中任取一点N.
如图在以OA为半径的半圆M中,有三个半径为1的相同的半圆,在半圆M中任取一点N.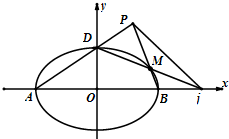 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,-2),且离心率为$\frac{{\sqrt{5}}}{3}$.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,-2),且离心率为$\frac{{\sqrt{5}}}{3}$.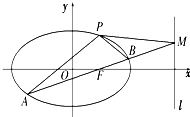 已知点p(c,$\frac{3}{2}$c)在以F(c,0)为右焦点的椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,斜率为1的直线m过点F与椭圆Γ交于A,B两点,且与直线l:x=4c交于点M.
已知点p(c,$\frac{3}{2}$c)在以F(c,0)为右焦点的椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,斜率为1的直线m过点F与椭圆Γ交于A,B两点,且与直线l:x=4c交于点M.