题目内容
18.椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,过椭圆右焦点F且斜率为I的直线l截椭圆所得弦长为$\frac{24}{7}$(Ⅰ)求椭圆C的方程;
(Ⅱ)已知A、B为椭圆长轴的两个端点,作不平行于坐标轴且不经过右焦点F的割线PQ,若满足∠AFP=∠BFQ,求证:割线PQ恒经过一定点.
分析 (1)写出直线l的方程y=x-c,由e=$\frac{1}{2}$及隐含条件得到a、b与c的关系,把椭圆方程化为仅含有c的表达式,联立直线l的方程和椭圆方程,由弦长公式求得c值,则椭圆方程可求;
(2)设P(x3,y3),Q(x4,y4),且割线PQ的方程为y=kx+m(k≠0),联立直线和椭圆方程,利用根与系数关系得到P,Q两点横坐标的和与积.结合∠AFP=∠BFQ,得$\frac{{y}_{1}}{{x}_{1}-1}+\frac{{y}_{2}}{{x}_{2}-1}=0$,整理后再与根与系数的关系联立得到m=-4k.代入割线方程,由直线系方程得答案.
解答 解:(Ⅰ)依题意设l:y=x-c,①
又e=$\frac{1}{2}$,∴$\frac{c}{a}=\frac{1}{2}$,a=2c,b2=a2-c2=3c2,
∴椭圆C:$\frac{{x}^{2}}{4{c}^{2}}+\frac{{y}^{2}}{3{c}^{2}}=1$,②
联立①②,得7x2-8cx-8c2=0.
∴x1+x2=$\frac{8c}{7}$,x1x2=$-\frac{8{c}^{2}}{7}$.
∴$\sqrt{2}•\sqrt{(\frac{8}{7}c)^{2}-4•(-\frac{8{c}^{2}}{7})}=\frac{24}{7}$,解得c=1.
∴$a=2,b=\sqrt{3}$.
于是C的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(Ⅱ)设P(x3,y3),Q(x4,y4),且割线PQ的方程为y=kx+m(k≠0),
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=kx+m}\end{array}\right.$,得(3+4k2)x2+8kmx+4m2-12=0.
∴x3+x4=$-\frac{8km}{3+4{k}^{2}}$,${x}_{3}{x}_{4}=\frac{4{m}^{2}-12}{3+4{k}^{2}}$(*).
由∠AFP=∠BFQ,得kPF=-kOF,∴$\frac{{y}_{3}}{{x}_{3}-1}+\frac{{y}_{4}}{{x}_{4}-1}=0$,
即y3(x4-1)+y4(x3-1)=0.
即2kx3x4+(m-k)(x3+x4)-2m=0.
将(*)代入上式得:$2k\frac{4{m}^{2}-12}{3+4{k}^{2}}+(m-k)\frac{-8km}{3+4{k}^{2}}-2m=0$,
化简得:m=-4k.
∴割线PQ的方程为y=k(x-4),则割线PQ恒经过一定点(4,0).
点评 本题主要考查了直线与椭圆的位置关系的应用,直线与曲线联立,根据方程的根与系数的关系解题,是处理这类问题的最为常用的方法,考查了直线恒过定点问题,该题是中档题.

| A. | (π,$\frac{9π}{8}$) | B. | [π,$\frac{9π}{8}$] | C. | [$\frac{7π}{6}$,$\frac{4π}{3}$] | D. | ($\frac{7π}{6}$,$\frac{4π}{3}$) |
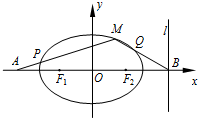 在平面直角坐标系xOy中,设中心在坐标原点的椭圆C的左、右焦点分别为F1、F2,右准线l:x=m+1与x轴的交点为B,BF2=m.
在平面直角坐标系xOy中,设中心在坐标原点的椭圆C的左、右焦点分别为F1、F2,右准线l:x=m+1与x轴的交点为B,BF2=m.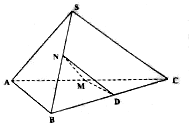 已知三棱锥S-ABC中△SAB与△ABC均为等边三角形,M、N分别为AC、SB的中点,经过M、N且与AB平行的平面α与BC交于点D.
已知三棱锥S-ABC中△SAB与△ABC均为等边三角形,M、N分别为AC、SB的中点,经过M、N且与AB平行的平面α与BC交于点D.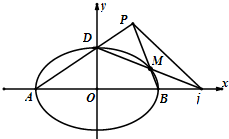 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,-2),且离心率为$\frac{{\sqrt{5}}}{3}$.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,-2),且离心率为$\frac{{\sqrt{5}}}{3}$.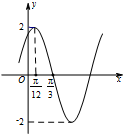 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.