题目内容
20.若函数f(x)=4x3-ax+3在[-$\frac{1}{2}$,$\frac{1}{2}$]上是单调函数,则实数a的取值范围是a≤0或a≥3.分析 求出函数的导函数,函数f(x)=4x3-ax+3在[-$\frac{1}{2}$,$\frac{1}{2}$]上是单调函数,所以f′(x)在[-$\frac{1}{2}$,$\frac{1}{2}$]符号不变,分离变量后利用函数的单调性求实数a的范围.
解答 解:由f(x)=4x3-ax+3,所以f′(x)=12x2-a,
因为函数f(x)=4x3-ax+3在[-$\frac{1}{2}$,$\frac{1}{2}$]上是单调函数,
所以以f′(x)=12x2-a在[-$\frac{1}{2}$,$\frac{1}{2}$]上符号不变,可得-a≥0或12×$(\frac{1}{2})^{2}-a≤0$恒成立.
解得a≤0或a≥3.
故答案为:a≤0或a≥3.
点评 本题考查了函数的单调性与函数的导函数的关系,二次函数的简单性质的应用,考查了利用函数的单调性求函数的最值,是中档题.

练习册系列答案
相关题目
6.设等差数列{an}满足$\frac{si{n}^{2}{a}_{4}-co{s}^{2}{a}_{4}+co{s}^{2}{a}_{4}co{s}^{2}{a}_{8}-si{n}^{2}{a}_{4}si{n}^{2}{a}_{8}}{sin({a}_{5}+{a}_{7})}$=1,公差d∈(-1,0),若当且仅当n=9时,数列{an}的前n项和Sn取得最大值,则首项a1的取值范围是( )
| A. | (π,$\frac{9π}{8}$) | B. | [π,$\frac{9π}{8}$] | C. | [$\frac{7π}{6}$,$\frac{4π}{3}$] | D. | ($\frac{7π}{6}$,$\frac{4π}{3}$) |
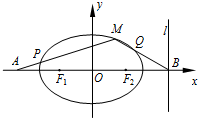 在平面直角坐标系xOy中,设中心在坐标原点的椭圆C的左、右焦点分别为F1、F2,右准线l:x=m+1与x轴的交点为B,BF2=m.
在平面直角坐标系xOy中,设中心在坐标原点的椭圆C的左、右焦点分别为F1、F2,右准线l:x=m+1与x轴的交点为B,BF2=m. 如图在以OA为半径的半圆M中,有三个半径为1的相同的半圆,在半圆M中任取一点N.
如图在以OA为半径的半圆M中,有三个半径为1的相同的半圆,在半圆M中任取一点N.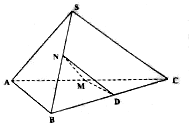 已知三棱锥S-ABC中△SAB与△ABC均为等边三角形,M、N分别为AC、SB的中点,经过M、N且与AB平行的平面α与BC交于点D.
已知三棱锥S-ABC中△SAB与△ABC均为等边三角形,M、N分别为AC、SB的中点,经过M、N且与AB平行的平面α与BC交于点D.