Question

【题目】已知函数y＝f(x)在定义域[－1，1]上既是奇函数，又是减函数．

(1)求证：对任意x1，x2∈[－1，1]，有[f(x1)＋f(x2)]·(x1＋x2)≤0；

(2)若f(1－a)＋f(1－a2)＜0，求实数a的取值范围．

Answer 1

【答案】（1）见解析；（2）0≤a＜1.

【解析】试题分析：（1）由x2∈[﹣1，1]，可得﹣x2∈[﹣1，1]，利用函数y=f（x）在定义域[﹣1，1]上是奇函数，又是减函数，即可证明结论；（2）f（1﹣a）+f（1﹣a2）＜0，等价于a2+a﹣2＜0，即可求出实数a的取值范围．

解析：

(1)证明：若x1＋x2＝0，显然不等式成立．

若x1＋x2＜0，则－1≤x1＜－x2≤1，

因为f(x)在[－1，1]上是减函数且为奇函数，

所以f(x1)＞f(－x2)＝－f(x2)，所以f(x1)＋f(x2)＞0.

所以[f(x1)＋f(x2)](x1＋x2)＜0成立．

若x1＋x2＞0，则1≥x1＞－x2≥－1，

同理可证f(x1)＋f(x2)＜0.

所以[f(x1)＋f(x2)](x1＋x2)＜0成立．

综上得证，对任意x1，x2∈[－1，1]，有[f(x1)＋f(x2)]·(x1＋x2)≤0恒成立．

(2)因为f(1－a)＋f(1－a2)＜0f(1－a2)＜－f(1－a)＝f(a－1)，

所以由f(x)在定义域[－1，1]上是减函数，得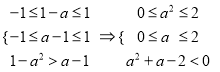

解得0≤a＜1.