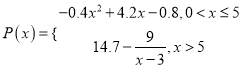题目内容
【题目】设函数![]() ,
,
(1)若f(1)<0,试判断函数单调性并求使不等式![]() 恒成立的
恒成立的![]() 的取值范围;
的取值范围;
(2)若![]() ,
, ![]() 且
且![]() 在
在![]() 上的最小值为-2,求m的值。
上的最小值为-2,求m的值。
【答案】(1)![]() (2)m=2
(2)m=2
【解析】试题分析:)利用条件![]() ,得到0<a<1.f(x)在R上单调递减,从而将
,得到0<a<1.f(x)在R上单调递减,从而将![]() 转化为
转化为![]() ,进而得
,进而得![]() ,研究二次函数得到本题结论;
,研究二次函数得到本题结论;
(2)令![]() ,得到二次函数h(t)=t2-2mt+2=(t-m)2+2-m2 (t≥
,得到二次函数h(t)=t2-2mt+2=(t-m)2+2-m2 (t≥![]() ),分类讨论研究得到m=2,得到本题结论.
),分类讨论研究得到m=2,得到本题结论.
试题解析:
(1) ![]() ,
,
∵![]()
∴![]()
∴0<a<1,
∵![]() 单调递减,
单调递减, ![]() 单调递增,故f(x)在R上单调递减.
单调递增,故f(x)在R上单调递减.
不等式化为![]()
![]()
![]() ,解得
,解得![]()
![]()
![]()
![]() .
.
![]() ,由(1)可知
,由(1)可知![]() 为增函数
为增函数
![]() 令h(t)=t2-2mt+2=(t-m)2+2-m2 (t≥
令h(t)=t2-2mt+2=(t-m)2+2-m2 (t≥![]() )
)
若m≥![]() ,当t=m时,h(t)min=2-m2=-2,∴m=2
,当t=m时,h(t)min=2-m2=-2,∴m=2
若m<![]() ,当t=
,当t=![]() 时,h(t)min=
时,h(t)min=![]() -3m=-2,解得m=
-3m=-2,解得m=![]() >
>![]() ,舍去
,舍去
综上可知m=2 .

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
【题目】随机调查某社区80个人,以研究这一社区居民的休闲方式是否与性别有关,得到下面的数据表:
休闲方式 | 看电视 | 运动 | 合计 |
男性 | 20 | 10 | 30 |
女性 | 45 | 5 | 50 |
合计 | 65 | 15 | 80 |
(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人是以运动为休闲方式的人数为随机变量X,求X的分布列和期望;
(2)根据以上数据,能否有99%的把握认为休闲方式与性别有关系?
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() ),其中n=a+b+c+d)
),其中n=a+b+c+d)