题目内容
【题目】如图所示,已知三棱锥P-ABC,∠ACB=90°,CB=4,AB=20,D为AB的中点,且△PDB是正三角形,PA⊥PC.
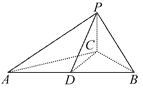
(1)求证:平面PAC⊥平面ABC.
(2)求二面角D-AP-C的正弦值.
【答案】(1)详见解析(2)![]()
【解析】试题分析:(1)在△APB中可证得AP⊥PB,再由条件可证得AP⊥平面PBC,从而得AP⊥BC,又AC⊥BC,AP∩AC=A,故可得BC⊥平面PAC,可得平面PAC⊥平面ABC. (2) 由PA⊥PC,PA⊥PB,可得∠BPC是二面角D-AP-C的平面角,在![]() 中,可得
中,可得![]() 即为所求。
即为所求。
试题解析:
(1)因为D是AB的中点,△PDB是正三角形,AB=20,
所以PD=![]() AB=10,
AB=10,
所以AP⊥PB.
又AP⊥PC,PB∩PC=P,
所以AP⊥平面PBC.
又BC平面PBC,
所以AP⊥BC.
又AC⊥BC,AP∩AC=A,
所以BC⊥平面PAC.
又BC平面ABC,
所以平面PAC⊥平面ABC.
(2)因为PA⊥PC,且PA⊥PB,
所以∠BPC是二面角D-AP-C的平面角.
由(1)知BC⊥平面PAC,
则BC⊥PC,
在![]() 中,
中, ![]()
所以![]() 。
。
所以二面角D-AP-C的正弦值为![]() 。
。

 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
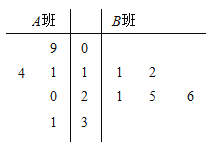
单元加期末复习先锋大考卷系列答案【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
立定跳远 (单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30秒跳绳 (单位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a-1 | b | 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则( )
A. 2号学生进入30秒跳绳决赛 B. 5号学生进入30秒跳绳决赛
C. 8号学生进入30秒跳绳决赛 D. 9号学生进入30秒跳绳决赛