题目内容
【题目】已知函数f(x)=|ax-2|,不等式f(x)≤4的解集为{x|-2≤x≤6}.
(1)求实数a的值;
(2)设g(x)=f(x)+f(x+3),若存在x∈R,使g(x)-tx≤2成立,求实数t的取值范围.
【答案】(1)1;(2)![]() .
.
【解析】
(1)利用绝对值不等式的解法求得-2≤![]()
![]() ≤6,对
≤6,对![]() 的正负分类讨论,结合不等式
的正负分类讨论,结合不等式![]() 的解集为
的解集为![]() 列方程,即可得解
列方程,即可得解
(2)由(1)可得![]() ,将
,将![]() 转化成
转化成![]() ,分别作出
,分别作出![]() 及
及![]() 的简图,“存在
的简图,“存在![]() ,使
,使![]() 成立”,转化成
成立”,转化成![]() 的图象与直线y=tx+2相交,由图列不等式即可得解。
的图象与直线y=tx+2相交,由图列不等式即可得解。
(1)由|![]()
![]() -2|≤4得-4≤
-2|≤4得-4≤![]()
![]() -2≤4,即-2≤
-2≤4,即-2≤![]()
![]() ≤6,
≤6,
当![]() >0时,
>0时,![]() ,所以
,所以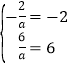 ,解得
,解得![]() =1;
=1;
当![]() <0时,
<0时,![]() ,所以
,所以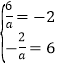 ,无解.
,无解.
所以实数![]() 的值为1.
的值为1.
(2)由已知g(x)=f(x)+f(x+3)=|x+1|+|x-2|=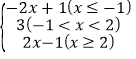 ,
,
不等式g(x)-tx≤2转化成g(x)≤tx+2,
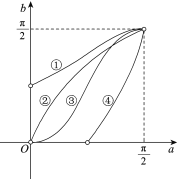
由题意知![]() 的图象与直线y=tx+2相交,作出对应图象
的图象与直线y=tx+2相交,作出对应图象
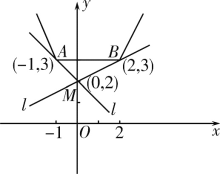
由图得,当t<0时,t≤kAM;当t>0时,t≥kBM,
又因为kAM=-1,![]() ,
,
所以t≤-1或![]() ,
,
即t∈(-∞,-1]∪[![]() ,+∞).
,+∞).

练习册系列答案
相关题目
【题目】为了调查生活规律与患胃病是否与有关,某同学在当地随机调查了200名30岁以上的人,并根据调查结果制成了不完整的列联表如下:
不患胃病 | 患胃病 | 总计 | |
生活有规律 | 60 | 40 | |
生活无规律 | 60 | 100 | |
总计 | 100 |
(1)补全列联表中的数据;
(2)用独性检验的基本原理,说明生活无规律与患胃病有关时,出错的概率不会超过多少?
参考公式和数表如下:
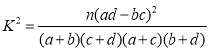
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |