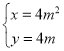题目内容
【题目】已知函数f(x)=2x-1,![]() (a∈R),若对任意x1∈[1,+∞),总存在x2∈R,使f(x1)=g(x2),则实数a的取值范围是( )
(a∈R),若对任意x1∈[1,+∞),总存在x2∈R,使f(x1)=g(x2),则实数a的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
对a分类讨论,分别求出函数f(x)和![]() 的值域,比较两个函数的值域即得解.
的值域,比较两个函数的值域即得解.
当a=0时,函数f(x)=2x-1的值域为[1,+∞),函数 ![]() 的值域为[0,+ +∞)满足题意.
的值域为[0,+ +∞)满足题意.
当a<0时,y=![]() 的值域为(2a,+∞),y=
的值域为(2a,+∞),y=![]() 的值域为[a+2,-a+2],
的值域为[a+2,-a+2],
因为a+2-2a=2-a>0,所以a+2>2a,所以此时函数g(x)的值域为(2a,+∞),由题得2a<1,即a<![]() ,即a<0.
,即a<0.
当a>0时,y=![]() 的值域为(2a,+∞), y=
的值域为(2a,+∞), y=![]() 的值域为[-a+2,a+2],
的值域为[-a+2,a+2],
当a≥![]() 时,-a+2≤2a,由题得
时,-a+2≤2a,由题得![]() .
.
当0<a<![]() 时,-a+2>2a,由题得2a<1,所以a<
时,-a+2>2a,由题得2a<1,所以a<![]() .所以0<a<
.所以0<a<![]() .
.
综合得a的范围为a<![]() 或1≤a≤2.
或1≤a≤2.
故选:C

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目