题目内容
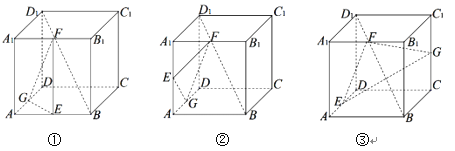
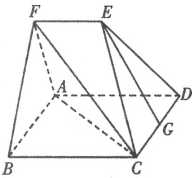
【题目】如图所示的多面体![]() 中,四边形
中,四边形![]() 为菱形,且
为菱形,且![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连结BD,交AC于M,连结FM,MG,证明![]() 即可解决问题。
即可解决问题。
(2)建立空间直角坐标系,求得平面![]() 的一个法向量
的一个法向量![]() 及
及![]() ,利用空间向量夹角公式即可求得直线EC与平面ACF所成角的正弦值,问题得解
,利用空间向量夹角公式即可求得直线EC与平面ACF所成角的正弦值,问题得解
证明:(1)连结BD,交AC于M,连结FM,MG,
因为BC=AD=2EF,EF∥BC,BC∥AD,所以![]() ,
,
在△ACD中,M,G分别为AC,CD的中点,所以![]() ,
,
所以![]() ,所以四边形EFMG是平行四边形,
,所以四边形EFMG是平行四边形,
所以EG∥FM,
又因为FM![]() 平面ACF,EC
平面ACF,EC![]() 平面ACF,所以EG∥平面ACF.
平面ACF,所以EG∥平面ACF.
(2)取AB的中点O,连结FO,OC,
因为AF=BF=BC,∠ABC=60°,四边形ABCD为菱形,所以FO⊥AB,OC⊥AB,
因为平面ABF⊥平面ABCD,所以FO⊥平面ABCD,
故以O为原点,![]() ,
,![]() ,
,![]() 分别为x轴,y轴,z轴正方向建立空间直角坐标系,设AF=BF=BC=2EF=2.
分别为x轴,y轴,z轴正方向建立空间直角坐标系,设AF=BF=BC=2EF=2.
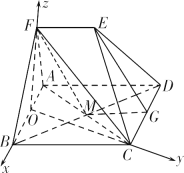
则A(-1,0,0),C(0,![]() ,0),F(0,0,
,0),F(0,0,![]() ),E(
),E(![]() ,
,![]() ,
,![]() ),
),![]() =(1,
=(1,![]() ,0),
,0),
![]() ,
,![]() ,
,
设![]() =
=![]() 是平面ACF的一个法向量,
是平面ACF的一个法向量,
则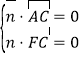 ,
,![]() ,
,
令y=z=1,则![]() ,故
,故![]() =(
=(![]() ,1,1),
,1,1),
设直线EC与平面ACF所成角为![]() ,
,
则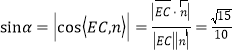 ,
,
所以直线EC与平面ACF所成角的正弦值为![]() .
.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目