题目内容
已知三棱锥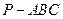 的四个顶点均在半径为3的球面上,且PA、PB、PC两两互相垂直,则三棱锥
的四个顶点均在半径为3的球面上,且PA、PB、PC两两互相垂直,则三棱锥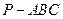 的侧面积的最大值为 .
的侧面积的最大值为 .
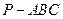 的四个顶点均在半径为3的球面上,且PA、PB、PC两两互相垂直,则三棱锥
的四个顶点均在半径为3的球面上,且PA、PB、PC两两互相垂直,则三棱锥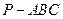 的侧面积的最大值为 .
的侧面积的最大值为 .18
依题意知,PA,PB,PC两两垂直,以PA,PB,PC为棱构造长方体,则该长方体的对角线即为球的直径,所以
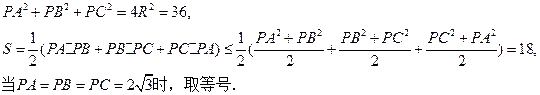
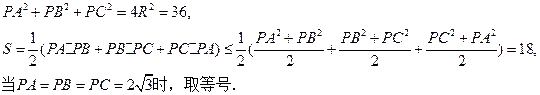

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
题目内容
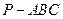 的四个顶点均在半径为3的球面上,且PA、PB、PC两两互相垂直,则三棱锥
的四个顶点均在半径为3的球面上,且PA、PB、PC两两互相垂直,则三棱锥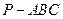 的侧面积的最大值为 .
的侧面积的最大值为 .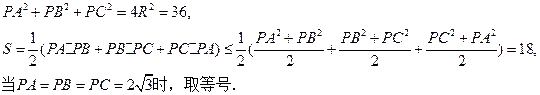

 轻松暑假总复习系列答案
轻松暑假总复习系列答案