题目内容
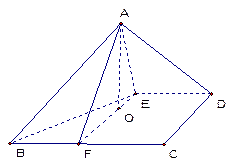
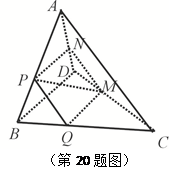
如图,在四面体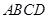 中,截面
中,截面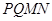 是正方形,则在下列命题中,错误的为( )
是正方形,则在下列命题中,错误的为( )
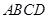 中,截面
中,截面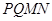 是正方形,则在下列命题中,错误的为( )
是正方形,则在下列命题中,错误的为( )A. |
B.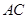 ∥截面 ∥截面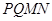 |
C.异面直线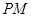 与 与 所成的角为 所成的角为 |
D.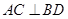 |

A
考点:
分析:首先由正方形中的线线平行推导线面平行,再利用线面平行推导线线平行,这样就把AC、BD平移到正方形内,即可利用平面图形知识做出判断.
解答:解:因为截面PQMN是正方形,所以PQ∥MN、QM∥PN,
则PQ∥平面ACD、QM∥平面BDA,
所以PQ∥AC,QM∥BD,
由PQ⊥QM可得AC⊥BD,故D正确;
由PQ∥AC可得AC∥截面PQMN,故B正确;
异面直线PM与BD所成的角等于PM与QM所成的角,故C正确;
综上A是错误的.
故选A.
点评:本题主要考查线面平行的性质与判定.
分析:首先由正方形中的线线平行推导线面平行,再利用线面平行推导线线平行,这样就把AC、BD平移到正方形内,即可利用平面图形知识做出判断.
解答:解:因为截面PQMN是正方形,所以PQ∥MN、QM∥PN,
则PQ∥平面ACD、QM∥平面BDA,
所以PQ∥AC,QM∥BD,
由PQ⊥QM可得AC⊥BD,故D正确;
由PQ∥AC可得AC∥截面PQMN,故B正确;
异面直线PM与BD所成的角等于PM与QM所成的角,故C正确;
综上A是错误的.
故选A.
点评:本题主要考查线面平行的性质与判定.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目

 中,
中,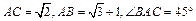 ,
,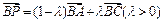 ,
,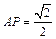 .
.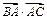 的值;
的值;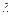 的值;
的值; AQ与BP交于点M,
AQ与BP交于点M,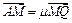 ,求实数
,求实数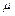 的值.
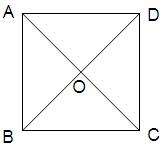
的值.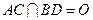 .将正方形ABCD沿对角线
.将正方形ABCD沿对角线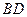 折起,使
折起,使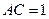 ,得到三棱锥A—BCD,如图所示.
,得到三棱锥A—BCD,如图所示.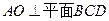 ;
;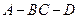 的余弦值.
的余弦值.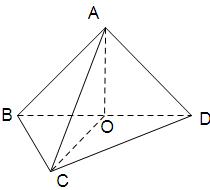

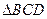 中,
中,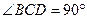 ,
,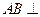 平面
平面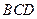 ,
,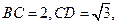
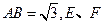 分别为
分别为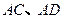 上的动点.
上的动点.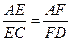 ,求证:平面
,求证:平面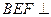 平面
平面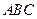 ;
;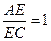 ,
,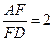 ,求平面
,求平面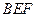 与平面
与平面
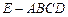 中,底面
中,底面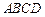 为矩形,平面
为矩形,平面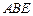 ,
,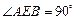 ,
,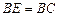 ,
,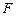 为
为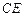 的中点,
的中点, 求证:
求证: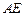 ∥平面
∥平面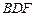 ;
;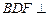 平面
平面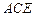 .
.
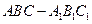 中,侧面
中,侧面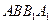 ,
,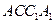 均为正方形,∠
均为正方形,∠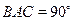 ,点
,点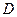 是棱
是棱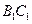 的中点.
的中点.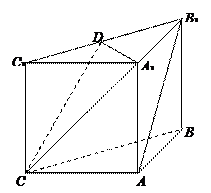
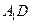 ⊥平面
⊥平面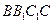 ;
;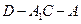 的余弦值.
的余弦值. 3分)如图6,正方形
3分)如图6,正方形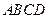 所在平面与圆
所在平面与圆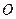 所在平面相交于
所在平面相交于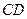 ,
,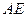 垂直于圆
垂直于圆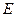 是圆
是圆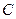 、
、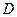 的点,
的点,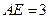 ,圆
,圆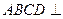 平面
平面 ;
;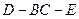 的平面角的正切值.
的平面角的正切值.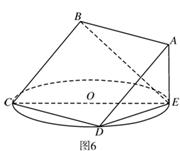
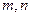 是两条不同的直线,
是两条不同的直线,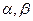 是两个不同的平面,
是两个不同的平面, 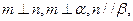 则
则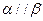
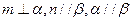 ,则
,则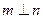
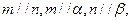 则
则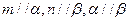 ,则
,则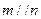
 中,
中,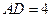 ,
, 、
、 分别是
分别是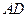 、
、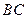 的中点,点
的中点,点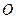 在
在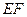 上,且
上,且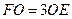 ,把
,把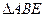 沿着
沿着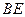 翻折,使点
翻折,使点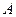 在平面
在平面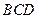 上的射影恰为点
上的射影恰为点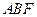
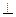
 平面
平面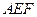 ;
; 的大小.
的大小.