题目内容
【题目】已知圆x2+y2=4上一定点A(2,0),B(1,1)为圆内一点,P,Q为圆上的动点. 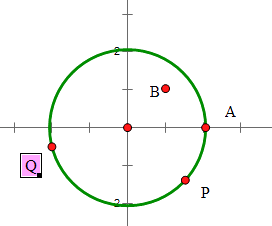
(1)求线段AP中点的轨迹方程;
(2)若∠PBQ=90°,求线段PQ中点的轨迹方程.
【答案】
(1)解:设AP中点为M(x,y),
由中点坐标公式可知,P点坐标为(2x﹣2,2y)
∵P点在圆x2+y2=4上,∴(2x﹣2)2+(2y)2=4.
故线段AP中点的轨迹方程为(x﹣1)2+y2=1
(2)解:设PQ的中点为N(x,y),
在Rt△PBQ中,|PN|=|BN|,
设O为坐标原点,则ON⊥PQ,
所以|OP|2=|ON|2+|PN|2=|ON|2+|BN|2,
所以x2+y2+(x﹣1)2+(y﹣1)2=4.
故线段PQ中点的轨迹方程为x2+y2﹣x﹣y﹣1=0.
【解析】(1)设出AP的中点坐标,利用中点坐标公式求出P的坐标,据P在圆上,将P坐标代入圆方程,求出中点的轨迹方程.(2)利用直角三角形的中线等于斜边长的一半得到|PN|=|BN|,利用圆心与弦中点连线垂直弦,利用勾股定理得到
|OP|2=|ON|2+|PN|2 , 利用两点距离公式求出动点的轨迹方程.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目