题目内容
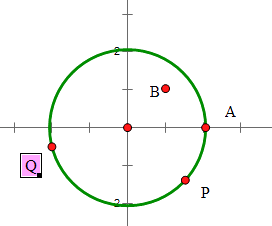
【题目】已知点A(0,2)为圆C:x2+y2﹣2ax﹣2ay=0(a>0)外一点,圆C上存在点P使得∠CAP=45°,则实数a的取值范围是( )
A.(0,1)
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:化圆的方程为标准方程可得(x﹣a)2+(y﹣a)2=2a2 ,
∴圆的圆心为C(a,a),半径r= ![]() |a|,
|a|,
∴AC= ![]() ,PC=
,PC= ![]() |a|,
|a|,
∵AC和PC长度固定,
∴当P为切点时,∠CAP最大,
∵圆C上存在点P使得∠CAP=45°,
∴若最大角度大于45°,则圆C上存在点P使得∠CAP=45°,
∴ ![]() =
= ![]() ≥sin∠CAP=sin45°=
≥sin∠CAP=sin45°= ![]() ,
,
整理可得a2+2a﹣2≥0,解得a≥ ![]() -1或a≤﹣
-1或a≤﹣ ![]() -1,
-1,
又 ![]() =
= ![]() ≤1,解得a≤1,
≤1,解得a≤1,
又点 A(0,2)为圆C:x2+y2﹣2ax﹣2ay=0外一点,
∴02+22﹣4a>0,解得a<1
∵a>0,∴综上可得 ![]() ﹣1≤a<1.
﹣1≤a<1.
故选B.

练习册系列答案
相关题目
【题目】某省的一个气象站观测点在连续4天里记录的![]() 指数
指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() (单位:
(单位: ![]() )的情况如表1:
)的情况如表1:
|
| 700 |
|
|
| 0.5 | 3.5 | 6.5 | 9.5 |
该省某市2017年9月![]() 指数频数分布如表2:
指数频数分布如表2:
|
|
|
|
|
|
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设![]() ,根据表1的数据,求出
,根据表1的数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)小李在该市开了一家洗车店,经统计,洗车店平均每天的收入与![]() 指数有相关关系,如表3:
指数有相关关系,如表3:
|
|
|
|
|
|
日均收入(元) |
|
|
|
|
|
根据表3估计小李的洗车店9月份平均每天的收入.
(附参考公式: ![]() ,其中
,其中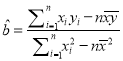 ,
, ![]() )
)