题目内容
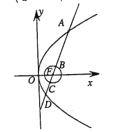
【题目】设![]() .
.
(1)求![]() 的反函数
的反函数![]() ;
;
(2)讨论![]() 在
在![]() 上的单调性,并加以证明;
上的单调性,并加以证明;
(3)令![]() ,当
,当![]() 时,
时,![]() 在
在![]() 上的值域是
上的值域是![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)令![]() ,由求反函数的规则解出
,由求反函数的规则解出![]() .
.
(2)复合函数,外层函数的单调性要由底数![]() 的取值范围确定,分两类讨论,内层函数的单调性可由定义法证明,再由复合函数的单调性判断出函数的单调性即可.
的取值范围确定,分两类讨论,内层函数的单调性可由定义法证明,再由复合函数的单调性判断出函数的单调性即可.
(3)分类讨论当![]() 时,和
时,和![]() 时两种情况,由(2)中单调性解出
时两种情况,由(2)中单调性解出![]() 的取值范围,并起来即可得到符合条件的参数的取值范围.
的取值范围,并起来即可得到符合条件的参数的取值范围.
(1)令![]() ,解得
,解得![]()
(2)令![]() ,设
,设![]()
![]() 在
在![]() 上单调递增.
上单调递增.
当![]() 时,根据复合函数单调性得到
时,根据复合函数单调性得到![]() 在
在![]() 上是减函数.
上是减函数.
当![]() 时,根据复合函数单调性得到
时,根据复合函数单调性得到![]() 在
在![]() 上是增函数.
上是增函数.
综上所述:当![]() 时,
时,![]() 在
在![]() 上是减函数;当
上是减函数;当![]() 时,
时, ![]() 在
在![]() 上是增函数.
上是增函数.
(3)当![]() 时,
时,![]() 在
在![]() 上是减函数,
上是减函数,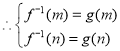
即有![]() 得
得![]() ,即
,即![]() ,
,
可知方程的两个根均大于1,故有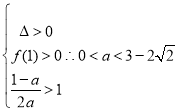
当![]() 时,
时,![]() 在
在![]() 上是增函数,
上是增函数,
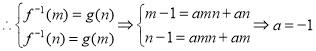 (舍去).
(舍去).
综上所述:![]() .
.

练习册系列答案
相关题目
【题目】一次数学知识竞赛中,两组学生成绩如下表:
分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
人数 | 甲组 | 2 | 5 | 10 | 13 | 14 | 6 |
乙组 | 4 | 4 | 16 | 2 | 12 | 12 | |
已经算得两个组的平均分都是80分,请根据你所学过的统计知识,进一步判断这两个组这次竞赛中成绩谁优谁次,并说明理由.