Question

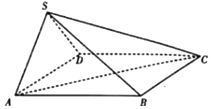
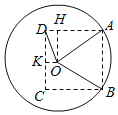
【题目】如图，圆O是一半径为10米的圆形草坪，为了满足周边市民跳广场舞的需要，现规划在草坪上建一个广场，广场形状如图中虚线部分所示的曲边四边形，其中A，B两点在⊙O上，A，B，C，D恰是一个正方形的四个顶点.根据规划要求，在A，B，C，D四点处安装四盏照明设备，从圆心O点出发，在地下铺设4条到A，B，C，D四点线路OA，OB，OC，OD.

（1）若正方形边长为10米，求广场的面积；

（2）求铺设的4条线路OA，OB，OC，OD总长度的最小值.

Answer 1

【答案】（1）100（平方米）（2）（米）

【解析】

（1）连接AB，广场面积等于正方形面积加上弓形面积，计算得到答案.

（2）过O作OK⊥CD，垂足为K，过O作OH⊥AD（或其延长线），垂足为H，设∠OAD＝θ（0＜θ），OD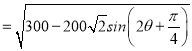，计算得到答案.

（1）连接AB，∵AB＝10，∴正方形ABCD的面积为100，

又OA＝OB＝10，∴△AOB为正三角形，则，

而圆的面积为100π，∴扇形AOB的面积为，

又三角形AOB的面积为.∴弓形面积为，

则广场面积为100（平方米）；

（2）过O作OK⊥CD，垂足为K，过O作OH⊥AD（或其延长线），垂足为H，

设∠OAD＝θ（0＜θ），则OH＝10sinθ，AH＝10cosθ，

∴DH＝|AD﹣AH|＝|2OH﹣AH|＝|20sinθ﹣10cosθ|，

∴OD.

∴当θ时，.

∴4条线路OA，OB，OC，OD总长度的最小值为（米）.