题目内容
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,且曲线
轴的正半轴为极轴建立极坐标系,且曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
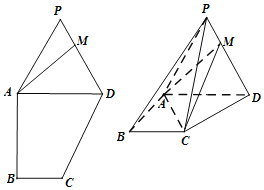
(2)设直线![]() 上的定点
上的定点![]() 在曲线
在曲线![]() 外且其到
外且其到![]() 上的点的最短距离为
上的点的最短距离为![]() ,试求点
,试求点![]() 的坐标.
的坐标.
【答案】(1)![]() 的普通方程为
的普通方程为![]() .
.![]() 的直角坐标方程为
的直角坐标方程为![]() (2)(-1,0)或(2,3)
(2)(-1,0)或(2,3)
【解析】
(1)对直线![]() 的参数方程
的参数方程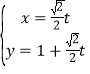 消参数
消参数![]() 即可求得直线
即可求得直线![]() 的普通方程,对
的普通方程,对![]() 整理并两边乘以
整理并两边乘以![]() ,结合
,结合![]() ,
,![]() 即可求得曲线
即可求得曲线![]() 的直角坐标方程。
的直角坐标方程。
(2)由(1)得:曲线C是以Q(1,1)为圆心,![]() 为半径的圆,设点P的坐标为
为半径的圆,设点P的坐标为![]() ,由题可得:
,由题可得:![]() ,利用两点距离公式列方程即可求解。
,利用两点距离公式列方程即可求解。
解:(1)由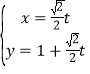 消去参数
消去参数![]() ,得
,得![]() .
.
即直线![]() 的普通方程为
的普通方程为![]() .
.
因为![]()
又![]() ,
,![]()
∴曲线![]() 的直角坐标方程为
的直角坐标方程为![]()
(2)由![]() 知,曲线C是以Q(1,1)为圆心,
知,曲线C是以Q(1,1)为圆心,![]() 为半径的圆
为半径的圆
设点P的坐标为![]() ,则点P到
,则点P到![]() 上的点的最短距离为|PQ|
上的点的最短距离为|PQ|![]()
![]()
即![]() ,整理得
,整理得![]() ,解得
,解得![]()
所以点P的坐标为(-1,0)或(2,3)

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
【题目】某企业为确定下一年投入某种产品的研发费用,需了解年研发费用![]() (单位:千万元)对年销售量
(单位:千万元)对年销售量![]() (单位:千万件)的影响,统计了近
(单位:千万件)的影响,统计了近![]() 年投入的年研发费用
年投入的年研发费用![]() 与年销售量
与年销售量![]() 的数据,得到散点图如图所示.
的数据,得到散点图如图所示.
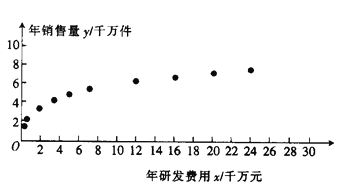
(1)利用散点图判断![]() 和
和![]() (其中
(其中![]() 均为大于
均为大于![]() 的常数)哪一个更适合作为年销售量
的常数)哪一个更适合作为年销售量![]() 和年研发费用
和年研发费用![]() 的回归方程类型(只要给出判断即可,不必说明理由)
的回归方程类型(只要给出判断即可,不必说明理由)
(2)对数据作出如下处理,令![]() ,得到相关统计量的值如下表:根据第(1)问的判断结果及表中数据,求
,得到相关统计量的值如下表:根据第(1)问的判断结果及表中数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
|
|
|
|
15 | 15 | 28.25 | 56.5 |
(3)已知企业年利润![]() (单位:千万元)与
(单位:千万元)与的关系为
![]() (其中
(其中![]() ),根据第(2)问的结果判断,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
),根据第(2)问的结果判断,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为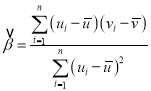 ,
,![]()