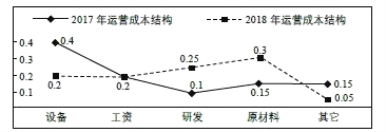
题目内容
【题目】如图,已知四边形ABCD是边长为2的菱形,∠ABC=60°,平面AEFC⊥平面ABCD,EF∥AC,AE=AB,AC=2EF.
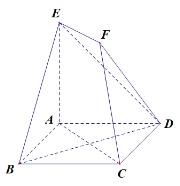
(1)求证:平面BED⊥平面AEFC;
(2)若四边形AEFC为直角梯形,且EA⊥AC,求二面角B-FC-D的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)首先根据题中条件证明线面垂直,然后根据线面垂直证明面面垂直.
(2)首先建立空间直角坐标系,然后求出点的坐标,求出平面法向量,利用二面角公式求出二面角的余弦值.
(1)因为四边形ABCD是边长为2的菱形,
所以![]() ,
,
又因为平面AEFC⊥平面ABCD,
平面AEFC![]() 平面ABCD
平面ABCD![]() ,
,
![]() 平面ABCD,所以
平面ABCD,所以![]() 平面AEFC,
平面AEFC,
又因为![]() 平面
平面![]() ,所以平面BED⊥平面AEFC.
,所以平面BED⊥平面AEFC.
(2)建立如图所示空间直角坐标系
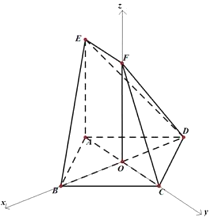
可知![]() ,
,![]() ,
,
点![]() ,
,
则![]() ,
,
设![]() 为平面
为平面![]() 的法向量,
的法向量,![]() 为平面
为平面![]() 的法向量,
的法向量,
由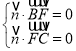 ,
,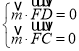 ,
,
解得![]() ,
,
设二面角B-FC-D为![]() ,
,
所以

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目