题目内容
【题目】已知函数![]() .
.
(Ⅰ)若![]() ,求曲线
,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)若![]() ,求证:
,求证:![]() ;
;
(Ⅲ)当![]() 时,若关于
时,若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的取值范围(用
的取值范围(用![]() 表示).
表示).
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析;(Ⅲ)当
;(Ⅱ)证明见解析;(Ⅲ)当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ,当
,当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() .
.
【解析】
(Ⅰ)求导求斜率,求函数值,利用点斜式求出切线方程;
(Ⅱ)当![]() 时,
时,![]() ,设
,设![]() ,求导得函数
,求导得函数![]() 的单调性与最值,得
的单调性与最值,得![]() ,即
,即![]() ,分析整理即可得出证明;
,分析整理即可得出证明;
(Ⅲ)由题意,![]() 在
在![]() 上有两个不相等的实数根
上有两个不相等的实数根![]() ,
,![]() ,令
,令![]() 得
得![]() 或
或![]() ;分类讨论得函数
;分类讨论得函数![]() 的单调性,进而得出结论.
的单调性,进而得出结论.
(Ⅰ)解:![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() ;
;
(Ⅱ)证明:当![]() 时,
时,![]() ,设
,设![]() ,所以
,所以![]() ,
,
![]() ,
,![]() 随
随![]() 变化情况如下:
变化情况如下:
|
| 0 |
|
|
| 0 |
|
| 递减 | 0 | 递增 |
由此可知对于![]() ,
,![]() ,即
,即![]() ,
,
因此![]() ,整理得
,整理得![]() ,即
,即![]() ;
;
(Ⅲ)由题意可知,即方程![]() 在
在![]() 上有两个不相等的实数根
上有两个不相等的实数根![]() ,
,![]() ,
,
令![]() .得
.得![]() 或
或![]() ;
;
当![]() 即
即![]() 时,在
时,在![]() 上
上![]() .所以
.所以![]() 是
是![]() 上的增函数,
上的增函数,
所以方程![]() 在
在![]() 上不可能有两个不相等的实数根;
上不可能有两个不相等的实数根;
当![]() 即
即![]() 时,在
时,在![]() 上
上![]() ,在
,在![]() 上
上![]() ,
,
所以![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
所以![]() ,
,
又因为![]() ,当
,当![]() 时,
时,![]() ,
,
(ⅰ)当![]() 即
即![]() 时,所以要使方程
时,所以要使方程![]() 有两个不相等的实数根,则
有两个不相等的实数根,则![]() 的取值范围是
的取值范围是![]() ;
;
(ⅱ)当![]() 即
即![]() 时,所以要使方程
时,所以要使方程![]() 有两个不相等的实数根,则
有两个不相等的实数根,则![]() 的取值范围是
的取值范围是![]() ;
;
综上所述,当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;当
;当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】我市某区2018年房地产价格因“棚户区改造”实行货币化补偿,使房价快速走高,为抑制房价过快上涨,政府从2019年2月开始采用实物补偿方式(以房换房),3月份开始房价得到很好的抑制,房价渐渐回落,以下是2019年2月后该区新建住宅销售均价的数据:
月份 | 3 | 4 | 5 | 6 | 7 |
价格 | 83 | 82 | 80 | 78 | 77 |
(1)研究发现,3月至7月的各月均价![]() (百元/平方米)与月份
(百元/平方米)与月份![]() 之间具有较强的线性相关关系,求价格
之间具有较强的线性相关关系,求价格![]() (百元/平方米)关于月份
(百元/平方米)关于月份![]() 的线性回归方程;
的线性回归方程;
(2)用![]() 表示用(1)中所求的线性回归方程得到的与
表示用(1)中所求的线性回归方程得到的与![]() 对应的销售均价的估计值,3月份至7月份销售均价估计值
对应的销售均价的估计值,3月份至7月份销售均价估计值![]() 与实际相应月份销售均价
与实际相应月份销售均价![]() 差的绝对值记为
差的绝对值记为![]() ,即
,即![]() ,
,![]() .若
.若![]() ,则将销售均价的数据
,则将销售均价的数据![]() 称为一个“好数据”,现从5个销售均价数据中任取
称为一个“好数据”,现从5个销售均价数据中任取
参考公式:回归方程系数公式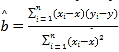 ,
,![]() ;参考数据:
;参考数据:![]() ,
,![]() .
.
【题目】为推动实施健康中国战略,树立国家大卫生、大健康概念,手机APP也推出了多款健康运动软件,如“微信运动”,杨老师的微信朋友圈内有![]() 位好友参与了“微信运动”,他随机选取了
位好友参与了“微信运动”,他随机选取了![]() 位微信好友(女
位微信好友(女![]() 人,男
人,男![]() 人),统计其在某一天的走路步数,其中,女性好友的走路步数数据记录如下:
人),统计其在某一天的走路步数,其中,女性好友的走路步数数据记录如下:
5860 | 8520 | 7326 | 6798 | 7325 | 8430 | 3216 | 7453 | 11754 | 9860 |
8753 | 6450 | 7290 | 4850 | 10223 | 9763 | 7988 | 9176 | 6421 | 5980 |
男性好友走路的步数情况可分为五个类别:![]() 步(说明“
步(说明“![]() ”表示大于等于
”表示大于等于![]() ,小于等于
,小于等于![]() ,下同),
,下同),![]() 步,
步,![]() 步,
步,![]() 步及以上,且
步及以上,且![]() 三种类别人数比例为
三种类别人数比例为![]() ,将统计结果绘制如图所示的条形图,若某人一天的走路步数超过
,将统计结果绘制如图所示的条形图,若某人一天的走路步数超过![]() 步被系统认定为“卫健型”,否则被系统认定为“进步型”.
步被系统认定为“卫健型”,否则被系统认定为“进步型”.
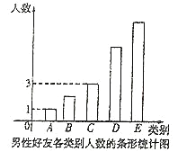
(1)若以杨老师选取的好友当天行走步数的频率分布来估计所有微信好友每日走路步数的概率分布,请估计杨老师的微信好友圈里参与“微信运动”的![]() 名好友中,每天走路步数在
名好友中,每天走路步数在![]() 步的人数;
步的人数;
(2)请根据选取的样本数据完成下面的![]() 列联表并据此判断能否有
列联表并据此判断能否有![]() 以上的把握认定“认定类型”与“性别”有关?
以上的把握认定“认定类型”与“性别”有关?
卫健型 | 进步型 | 总计 | |
男 | 20 | ||
女 | 20 | ||
总计 | 40 |
附: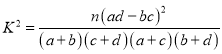 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |