题目内容
1.已知x,y满足$\left\{\begin{array}{l}2x+y+4≤0\\{(x+2)^2}+{(y+1)^2}≤1\end{array}\right.$,则x2+y2的取值范围是[$\frac{16}{5}$,6+2$\sqrt{5}$].分析 首先画出x,y满足的平面区域,结合x2+y2的几何意义求范围.
解答 解:由题意,x,y满足的平面区域如图阴影部分,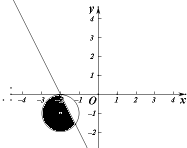 则在阴影部分(包括边界)的点中到原点距离,
则在阴影部分(包括边界)的点中到原点距离,
最小值为原点到直线的距离为:$\frac{4}{\sqrt{5}}=\frac{4\sqrt{5}}{5}$;
最大值为$\sqrt{(-2)^{2}+(-1)^{2}}+1$=1+$\sqrt{5}$,
所以x2+y2的取值范围是[$\frac{16}{5}$,6+2$\sqrt{5}$].
故答案为:[$\frac{16}{5}$,6+2$\sqrt{5}$].
点评 本题考查了线性规划的运用求两个变量的代数式的值的范围;关键正确画出不等式组表示的平面区域,利用x2+y2的几何意义求最值.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
9.下表为某班5位同学身高x(单位:cm)与体重y(单位kg)的数据,
若两个量间的回归直线方程为$\widehat{y}$=1.16x+a,则a的值为( )
| 身高 | 170 | 171 | 166 | 178 | 160 |
| 体重 | 75 | 80 | 70 | 85 | 65 |
| A. | -122.2 | B. | -121.04 | C. | -91 | D. | -92.3 |
16.a=$\frac{1}{2}$cos6°-$\frac{\sqrt{3}}{2}$sin6°,b=2sin13°cos13°,c=$\sqrt{\frac{1-cos50°}{2}}$,则( )
| A. | a<c<b | B. | a<b<c | C. | a>b>c | D. | b<c<a |
13.已知“x>k”是“$\frac{2-x}{x+1}$<0”的充分不必要条件,则k的取值范围是( )
| A. | [2,+∞) | B. | [1,+∞) | C. | (-1,+∞) | D. | (-∞,-1] |
10.等差数列{an}中,首项a1>0,公差d≠0,前n项和为Sn(n∈N*).有下列命题
①若S3=S11,则必有S14=0;
②若S3=S11,则必有S7是Sn中最大的项;
③若S7>S8,则必有S8>S9;
④若S7>S8,则必有S6>S9
其中正确的命题的个数是( )
①若S3=S11,则必有S14=0;
②若S3=S11,则必有S7是Sn中最大的项;
③若S7>S8,则必有S8>S9;
④若S7>S8,则必有S6>S9
其中正确的命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.已知a>b>c且a+b+c=0,则下列不等式恒成立的是( )
| A. | a2>b2>c2 | B. | a|b|>c|b| | C. | ac>bc | D. | ab>ac |
 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′分别交于M,N两点,设BM=x,x∈[0,1],给出以下四个结论:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′分别交于M,N两点,设BM=x,x∈[0,1],给出以下四个结论: