题目内容
3.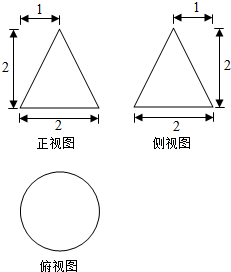 某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=$\frac{新工件的体积}{原工件的体积}$)( )
某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=$\frac{新工件的体积}{原工件的体积}$)( )| A. | $\frac{8}{9π}$ | B. | $\frac{16}{9π}$ | C. | $\frac{4(\sqrt{2}-1)^{3}}{π}$ | D. | $\frac{12(\sqrt{2}-1)^{3}}{π}$ |
分析 根据三视图可判断其为圆锥,底面半径为1,高为2,求解体积.
利用几何体的性质得出此长方体底面边长为n的正方形,高为x,
利用轴截面的图形可判断得出n=$\sqrt{2}$(1-$\frac{1}{2}x$),0<x<2,求解体积式子,利用导数求解即可,最后利用几何概率求解即.
解答 解:根据三视图可判断其为圆锥,
∵底面半径为1,高为2,
∴V=$\frac{1}{3}×π×{1}^{2}$×2=$\frac{2π}{3}$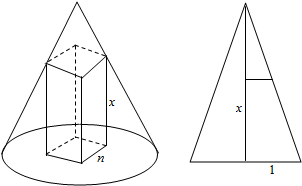
∵加工成一个体积尽可能大的长方体新工件,
∴此长方体底面边长为n的正方形,高为x,
∴根据轴截面图得出:$\frac{x}{2}$=$\frac{1-\frac{\sqrt{2}n}{2}}{1}$,
解得;n=$\sqrt{2}$(1-$\frac{1}{2}x$),0<x<2,
∴长方体的体积Ω=2(1-$\frac{1}{2}x$)2x,Ω′=$\frac{3}{2}$x2-4x+2,
∵,Ω′=$\frac{3}{2}$x2-4x+2=0,x=$\frac{2}{3}$,x=2,
∴可判断(0,$\frac{2}{3}$)单调递增,($\frac{2}{3}$,2)单调递减,
Ω最大值=2(1-$\frac{1}{2}×\frac{2}{3}$)2×$\frac{2}{3}$=$\frac{16}{27}$,
∴原工件材料的利用率为$\frac{\frac{16}{27}}{\frac{2π}{3}}$=$\frac{16}{27}$×$\frac{3}{2π}$=$\frac{8}{9π}$,
故选:A
点评 本题很是新颖,知识点融合的很好,把立体几何,导数,概率都相应的考查了,综合性强,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.如果函数f(x)=$\frac{1}{2}$(m-2)x2+(n-8)x+1(m≥0,n≥0)在区间[$\frac{1}{2},2$]上单调递减,那么mn的最大值为( )
| A. | 16 | B. | 18 | C. | 25 | D. | $\frac{81}{2}$ |
14.若变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≥1}\\{y-x≤1}\\{x≤1}\end{array}\right.$,则z=2x-y的最小值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
11.函数f(x)=ax3+bx2+cx+d的图象如图所示,则下列结论成立的是( )


| A. | a>0,b<0,c>0,d>0 | B. | a>0,b<0,c<0,d>0 | C. | a<0,b<0,c<0,d>0 | D. | a>0,b>0,c>0,d<0 |
18.设函数f(x)=ln(1+x)-ln(1-x),则f(x)是( )
| A. | 奇函数,且在(0,1)上是增函数 | B. | 奇函数,且在(0,1)上是减函数 | ||
| C. | 偶函数,且在(0,1)上是增函数 | D. | 偶函数,且在(0,1)上是减函数 |