题目内容
11．函数f（x）=ax3+bx2+cx+d的图象如图所示，则下列结论成立的是（ ）
| A． | a＞0，b＜0，c＞0，d＞0 | B． | a＞0，b＜0，c＜0，d＞0 | C． | a＜0，b＜0，c＜0，d＞0 | D． | a＞0，b＞0，c＞0，d＜0 |
分析 根据函数的图象和性质，利用排除法进行判断即可．
解答 解：f（0）=d＞0，排除D，
当x→+∞时，y→+∞，∴a＞0，排除C，
函数的导数f′（x）=3ax2+2bx+c，
则f′（x）=0有两个不同的正实根，
则x1+x2=-$\frac{2b}{3a}$＞0且x1x2=$\frac{c}{3a}$＞0，（a＞0），
∴b＜0，c＞0，
方法2：f′（x）=3ax2+2bx+c，
由图象知当当x＜x1时函数递增，当x1＜x＜x2时函数递减，则f′（x）对应的图象开口向上，
则a＞0，且x1+x2=-$\frac{2b}{3a}$＞0且x1x2=$\frac{c}{3a}$＞0，（a＞0），
∴b＜0，c＞0，
故选：A
点评 本题主要考查函数图象的识别和判断，根据函数图象的信息，结合函数的极值及f（0）的符号是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
1．已知某批零件的长度误差（单位：毫米）服从正态分布N（0，32），从中随机抽取一件，其长度误差落在区间（3，6）内的概率为（ ）
（附：若随机变量ξ服从正态分布N（μ，σ2），则P（μ-σ＜ξ＜μ+σ）=68.26%，P（μ-2σ＜ξ＜μ+2σ）=95.44%）
（附：若随机变量ξ服从正态分布N（μ，σ2），则P（μ-σ＜ξ＜μ+σ）=68.26%，P（μ-2σ＜ξ＜μ+2σ）=95.44%）
| A． | 4.56% | B． | 13.59% | C． | 27.18% | D． | 31.74% |
6．设i是虚数单位，则复数（1-i）（1+2i）=（ ）
| A． | 3+3i | B． | -1+3i | C． | 3+i | D． | -1+i |
16．执行如图所示的程序框图，如果输入n=3，则输出的S=（ ）
| A． | $\frac{6}{7}$ | B． | $\frac{3}{7}$ | C． | $\frac{8}{9}$ | D． | $\frac{4}{9}$ |
3．
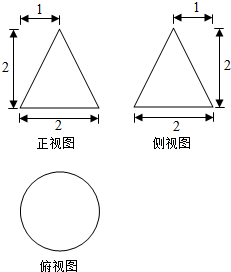某工件的三视图如图所示．现将该工件通过切削，加工成一个体积尽可能大的长方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件材料的利用率为（材料利用率=$\frac{新工件的体积}{原工件的体积}$）（ ）
某工件的三视图如图所示．现将该工件通过切削，加工成一个体积尽可能大的长方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件材料的利用率为（材料利用率=$\frac{新工件的体积}{原工件的体积}$）（ ）| A． | $\frac{8}{9π}$ | B． | $\frac{16}{9π}$ | C． | $\frac{4（\sqrt{2}-1）^{3}}{π}$ | D． | $\frac{12（\sqrt{2}-1）^{3}}{π}$ |