题目内容

18．设函数f（x）=ln（1+x）-ln（1-x），则f（x）是（　　）
A．奇函数，且在（0，1）上是增函数B．奇函数，且在（0，1）上是减函数
C．偶函数，且在（0，1）上是增函数D．偶函数，且在（0，1）上是减函数

分析 求出好的定义域，判断函数的奇偶性，以及函数的单调性推出结果即可．

解答 解：函数f（x）=ln（1+x）-ln（1-x），函数的定义域为（-1，1），
函数f（-x）=ln（1-x）-ln（1+x）=-[ln（1+x）-ln（1-x）]=-f（x），所以函数是奇函数．
排除C，D，正确结果在A，B，只需判断特殊值的大小，即可推出选项，x=0时，f（0）=0；
x=$\frac{1}{2}$时，f（$\frac{1}{2}$）=ln（1+$\frac{1}{2}$）-ln（1-$\frac{1}{2}$）=ln3＞1，显然f（0）＜f（$\frac{1}{2}$），函数是增函数，所以B错误，A正确．
故选：A．

点评 本题考查函数的奇偶性以及函数的单调性的判断与应用，考查计算能力．

练习册系列答案
相关题目
8．下列函数中，最小正周期为π且图象关于原点对称的函数是（　　）
A．y=cos（2x+$\frac{π}{2}$）B．y=sin（2x+$\frac{π}{2}$）C．y=sin2x+cos2xD．y=sinx+cosx
9．2-3，${3}^{\frac{1}{2}}$，log25三个数中最大数的是log25．
6．设i是虚数单位，则复数（1-i）（1+2i）=（　　）
A．3+3iB．-1+3iC．3+iD．-1+i
13．在平面直角坐标系xOy中，若直线y=2a与函数y=|x-a|-1的图象只有一个交点，则a的值为$-\frac{1}{2}$．
3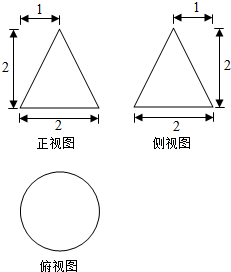． 某工件的三视图如图所示．现将该工件通过切削，加工成一个体积尽可能大的长方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件材料的利用率为（材料利用率=$\frac{新工件的体积}{原工件的体积}$）（　　）
A．$\frac{8}{9π}$B．$\frac{16}{9π}$C．$\frac{4（\sqrt{2}-1）^{3}}{π}$D．$\frac{12（\sqrt{2}-1）^{3}}{π}$
10．若复数z=i（3-2i）（i是虚数单位），则$\overline{z}$=（　　）
A．2-3iB．2+3iC．3+2iD．3-2i
7．已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{6}}{3}$，若原点O到直线x+y-b=0的距离为$\sqrt{2}$，求椭圆的方程．
8．如图的矩形长为5，宽为2，在矩形内随机地撒300颗黄豆，数得落在阴影部分的黄豆数为138颗，由此我们可以估计出阴影部分的面积约为4.6．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网