题目内容
15.在($\sqrt{x}$-1)4的展开式中,x的系数为6.分析 根据题意二项式($\sqrt{x}$-1)4的展开式的通项公式为Tr+1=${C}_{4}^{r}$•(-1)r•${x}^{2-\frac{r}{2}}$,分析可得,r=2时,有x的项,将r=2代入可得答案.
解答 解:二项式($\sqrt{x}$-1)4的展开式的通项公式为Tr+1=${C}_{4}^{r}$•(-1)r•${x}^{2-\frac{r}{2}}$,
令2-$\frac{r}{2}$=1,求得r=2,
∴二项式($\sqrt{x}$-1)4的展开式中x的系数为${C}_{4}^{2}$=6,
故答案为:6.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,属于中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.设i是虚数单位,则复数(1-i)(1+2i)=( )
| A. | 3+3i | B. | -1+3i | C. | 3+i | D. | -1+i |
3.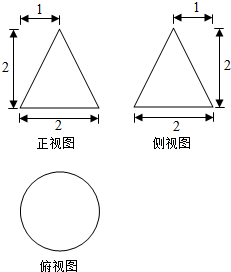 某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=$\frac{新工件的体积}{原工件的体积}$)( )
某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=$\frac{新工件的体积}{原工件的体积}$)( )
 某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=$\frac{新工件的体积}{原工件的体积}$)( )
某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=$\frac{新工件的体积}{原工件的体积}$)( )| A. | $\frac{8}{9π}$ | B. | $\frac{16}{9π}$ | C. | $\frac{4(\sqrt{2}-1)^{3}}{π}$ | D. | $\frac{12(\sqrt{2}-1)^{3}}{π}$ |
10.若复数z=i(3-2i)(i是虚数单位),则$\overline{z}$=( )
| A. | 2-3i | B. | 2+3i | C. | 3+2i | D. | 3-2i |
5.若等比数列{an}中,a2+a5+a11=2,a5+a8+a14=6,则a2+a5+a8+a11+a14的值为( )
| A. | 8 | B. | 大于8 | C. | $\frac{242}{31}$ | D. | $\frac{240}{41}$ |