题目内容
13.如果函数f(x)=$\frac{1}{2}$(m-2)x2+(n-8)x+1(m≥0,n≥0)在区间[$\frac{1}{2},2$]上单调递减,那么mn的最大值为( )| A. | 16 | B. | 18 | C. | 25 | D. | $\frac{81}{2}$ |
分析 函数f(x)=$\frac{1}{2}$(m-2)x2+(n-8)x+1(m≥0,n≥0)在区间[$\frac{1}{2},2$]上单调递减,则f′(x)≤0,故(m-2)x+n-8≤0在[$\frac{1}{2}$,2]上恒成立.而(m-2)x+n-8是一次函数,在[$\frac{1}{2}$,2]上的图象是一条线段.故只须在两个端点处f′($\frac{1}{2}$)≤0,f′(2)≤0即可.结合基本不等式求出mn的最大值.
解答 解:∵函数f(x)=$\frac{1}{2}$(m-2)x2+(n-8)x+1(m≥0,n≥0)在区间[$\frac{1}{2},2$]上单调递减,
∴f′(x)≤0,故(m-2)x+n-8≤0在[$\frac{1}{2}$,2]上恒成立.而(m-2)x+n-8是一次函数,在[$\frac{1}{2}$,2]上的图象是一条线段.故只须在两个端点处f′($\frac{1}{2}$)≤0,f′(2)≤0即可.即
$\left\{\begin{array}{l}{\frac{1}{2}(m-2)+n-8≤0(1)}\\{2(m-2)+n-8≤0(2)}\end{array}\right.$
由(2)得m≤$\frac{1}{2}$(12-n),
∴mn≤$\frac{1}{2}$n(12-n)≤$\frac{1}{2}$$(\frac{n+12-n}{2})^{2}$=18,当且仅当m=3,n=6时取得最大值,经检验m=3,n=6满足(1)和(2).
故选:B.
解法二:
∵函数f(x)=$\frac{1}{2}$(m-2)x2+(n-8)x+1(m≥0,n≥0)在区间[$\frac{1}{2},2$]上单调递减,
∴①m=2,n<8
对称轴x=-$\frac{n-8}{m-2}$,
②$\left\{\begin{array}{l}{m-2>0}\\{-\frac{n-8}{m-2}≥2}\end{array}\right.$即$\left\{\begin{array}{l}{m>2}\\{2m+n-12≤0}\end{array}\right.$
③$\left\{\begin{array}{l}{m-2<0}\\{-\frac{n-8}{m-2}≤\frac{1}{2}}\end{array}\right.$即$\left\{\begin{array}{l}{m<2}\\{2n+m-18≤0}\end{array}\right.$
设$\left\{\begin{array}{l}{x>2}\\{2x+y-12≤0}\end{array}\right.$或$\left\{\begin{array}{l}{x<2}\\{2y+x-18≤0}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y<8}\end{array}\right.$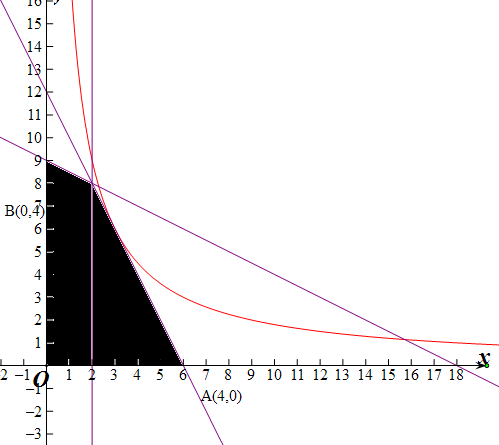
设y=$\frac{k}{x}$,y′=$-\frac{k}{{x}^{2}}$,
当切点为(x0,y0),k取最大值.
①-$\frac{k}{{{x}_{0}}^{2}}$=-2.k=2x${{\;}_{0}}^{2}$,
∴y0=-2x0+12,y0=$\frac{2{x}_{0}^{2}}{{x}_{0}}$=2x0,可得x0=3,y0=6,
∵x=3>2
∴k的最大值为3×6=18
②-$\frac{k}{{{x}_{0}}^{2}}$=-$\frac{1}{2}$.,k=$\frac{1}{2}{x}_{0}^{2}$,
y0=$\frac{\frac{1}{2}{x}_{0}^{\;}}{{x}_{0}}$=$\frac{1}{2}{x}_{0}$,
2y0+x0-18=0,
解得:x0=9,y0=$\frac{9}{2}$
∵x0<2
∴不符合题意.
③m=2,n=8,k=mn=16
综合得出:m=3,n=6时k最大值k=mn=18,
故选;B
点评 本题综合考查了函数方程的运用,线性规划问题,结合导数的概念,运用几何图形判断,难度较大,属于难题.

 阅读快车系列答案
阅读快车系列答案| A. | -2 | B. | -1 | C. | 2 | D. | 1 |
| A. | (1,3) | B. | (1,4) | C. | (2,3) | D. | (2,4) |
(附:若随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ<ξ<μ+σ)=68.26%,P(μ-2σ<ξ<μ+2σ)=95.44%)
| A. | 4.56% | B. | 13.59% | C. | 27.18% | D. | 31.74% |
| A. | y=cos(2x+$\frac{π}{2}$) | B. | y=sin(2x+$\frac{π}{2}$) | C. | y=sin2x+cos2x | D. | y=sinx+cosx |
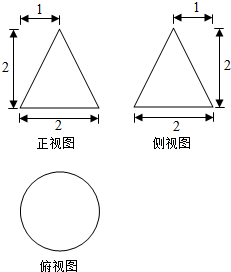 某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=$\frac{新工件的体积}{原工件的体积}$)( )
某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=$\frac{新工件的体积}{原工件的体积}$)( )| A. | $\frac{8}{9π}$ | B. | $\frac{16}{9π}$ | C. | $\frac{4(\sqrt{2}-1)^{3}}{π}$ | D. | $\frac{12(\sqrt{2}-1)^{3}}{π}$ |