题目内容
4.已知$α∈(\frac{3π}{2},2π)$,cosα=$\frac{4}{5}$,则cos(α+$\frac{π}{4}$)=$\frac{7\sqrt{2}}{10}$.分析 由同角三角函数的基本关系可得sinα,代入两角和的余弦公式可得.
解答 解:∵$α∈(\frac{3π}{2},2π)$,cosα=$\frac{4}{5}$,
∴sinα=-$\sqrt{1-co{s}^{2}α}$=-$\frac{3}{5}$,
∴cos(α+$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$cosα-$\frac{\sqrt{2}}{2}$sinα
=$\frac{\sqrt{2}}{2}×\frac{4}{5}-\frac{\sqrt{2}}{2}×(-\frac{3}{5})$=$\frac{7\sqrt{2}}{10}$
故答案为:$\frac{7\sqrt{2}}{10}$.
点评 本题考查两角和与差的余弦公式,涉及同角三角函数的基本关系,属基础题.

练习册系列答案
相关题目
14.已知△ABC的三边满足(a+b+c)(a+b-c)=($\sqrt{3}$+2)ab,则角C等于( )
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
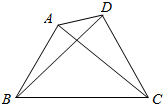 在四边形ABCD中,AB=$\sqrt{3}$,CD=2,∠BAD=135°,∠BCD=60°,∠ADB=30°.
在四边形ABCD中,AB=$\sqrt{3}$,CD=2,∠BAD=135°,∠BCD=60°,∠ADB=30°.