题目内容
14.已知$cosα=\frac{{\sqrt{5}}}{5}$,α是第四象限角,且tan(α+β)=1,则tanβ的值为-3.分析 由条件利用同角三角函数的基本关系求得 tanα 的值,再利用两角和的正切公式求得tanβ的值.
解答 解:∵已知$cosα=\frac{{\sqrt{5}}}{5}$,α是第四象限角,∴sinα=-$\sqrt{{1-cos}^{2}α}$=-$\frac{2\sqrt{5}}{5}$,∴tanα=$\frac{sinα}{cosα}$=-2,
再根据tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=$\frac{-2+tanβ}{1+2tanβ}$=1,求得tanβ=-3,
故答案为:-3.
点评 本题主要考查同角三角函数的基本关系,两角和的正切公式的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.(x-2y)7的展开式中的第4项为( )
| A. | -35x4y3 | B. | 280x4y3 | C. | -280x4y3 | D. | 35x4y3 |
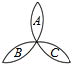 荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示,假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是$\frac{1}{3}$.
荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示,假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是$\frac{1}{3}$.