题目内容
1.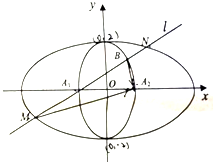 如图,焦点在x轴上的椭圆C1和焦点在y轴上的椭圆C2相切于点(0,2)、(0,-2),且椭圆C1,C2的离心率均为$\frac{\sqrt{3}}{2}$.
如图,焦点在x轴上的椭圆C1和焦点在y轴上的椭圆C2相切于点(0,2)、(0,-2),且椭圆C1,C2的离心率均为$\frac{\sqrt{3}}{2}$.(Ⅰ)求椭圆C1,C2的方程;
(Ⅱ)设椭圆C2的左、右顶点为A1,A2,过A1的直线l与椭圆C1,C2分别交于点M,N和A1,B(异于A2),若$\overrightarrow{B{A}_{2}}$•$\overrightarrow{M{A}_{2}}$=0,求直线l的方程.
分析 (Ⅰ)设椭圆C1和C2的方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{4}=1$,$\frac{{y}^{2}}{4}+\frac{{x}^{2}}{{b}^{2}}=1$,通过离心率可得各自的方程;
(Ⅱ)设l的方程为y=k(x+1),通过联立方程组$\left\{\begin{array}{l}{y=k(x+1)}\\{\frac{{y}^{2}}{4}+{x}^{2}=1}\end{array}\right.$、利用韦达定理、$\overrightarrow{B{A}_{2}}$•$\overrightarrow{M{A}_{2}}$=0,计算可得斜率k=±$\frac{\sqrt{119}}{4}$.
解答 解:(Ⅰ)设椭圆C1和C2的方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{4}=1$,$\frac{{y}^{2}}{4}+\frac{{x}^{2}}{{b}^{2}}=1$,
则$\frac{{a}^{2}-4}{{a}^{2}}$=$\frac{3}{4}$,即a2=16,
$\frac{4-{b}^{2}}{4}$=$\frac{3}{4}$,即b2=1,
所以椭圆C1和C2的方程为:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1$,$\frac{{y}^{2}}{4}+{x}^{2}=1$;
(Ⅱ)由(Ⅰ)知A1(-1,0),A2(1,0),
设l的方程为y=k(x+1),B(x1,y1),M(x2,y2),
联立方程组$\left\{\begin{array}{l}{y=k(x+1)}\\{\frac{{y}^{2}}{4}+{x}^{2}=1}\end{array}\right.$,消去y得(4+k2)x2+2k2x+k2-4=0,
∵过A1的直线l与椭圆C2分别交于点A1,B(异于A2),
∴x1=$-\frac{2{k}^{2}}{4+{k}^{2}}$+1=$\frac{4-{k}^{2}}{4+{k}^{2}}$,
∴y1=k(x1+1)=$\frac{8k}{4+{k}^{2}}$,即B($\frac{4-{k}^{2}}{4+{k}^{2}}$,$\frac{8k}{4+{k}^{2}}$),
∵$\overrightarrow{B{A}_{2}}$•$\overrightarrow{M{A}_{2}}$=0,
∴$\frac{{y}_{2}}{{x}_{2}-1}$•$\frac{\frac{8k}{4+{k}^{2}}}{\frac{4-{k}^{2}}{4+{k}^{2}}-1}$=-1,化简得y2=$\frac{k}{4}$(x2-1),
联立方程组$\left\{\begin{array}{l}{{y}_{2}=k({x}_{2}+1)}\\{{y}_{2}=\frac{k}{4}({x}_{2}-1)}\end{array}\right.$,解得$\left\{\begin{array}{l}{{x}_{2}=-\frac{5}{3}}\\{{y}_{2}=-\frac{2}{3}k}\end{array}\right.$,
代入方程$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1$,解得k=±$\frac{\sqrt{119}}{4}$,
所以直线l的方程为y=±$\frac{\sqrt{119}}{4}$(x+1).
点评 本题是一道直线与圆锥曲线的综合题,涉及到韦达定理,向量数量积运算等知识,注意解题方法的积累,属于中档题.

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案| A. | $\underset{\stackrel{1007}{π}}{k=1}$2k不能被10100整除 | |
| B. | $\frac{\underset{\stackrel{2015}{π}}{k=1}(4k-2)}{\underset{\stackrel{2014}{π}}{k=1}(2k-1)}$=22015 | |
| C. | $\underset{\stackrel{1008}{π}}{k=1}$(2k-1)不能被5100整除 | |
| D. | $\underset{\stackrel{1008}{π}}{k=1}$(2k-1)$\underset{\stackrel{1007}{π}}{k=1}$2k=$\underset{\stackrel{2015}{π}}{k=1}$k |
 某校在一次数学考试中随机抽取了N名学生的成绩并分成一下五组,第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,已知图中从左到右后3个小组的频率之比为3:2:1,其中第4组的频数为20.
某校在一次数学考试中随机抽取了N名学生的成绩并分成一下五组,第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,已知图中从左到右后3个小组的频率之比为3:2:1,其中第4组的频数为20.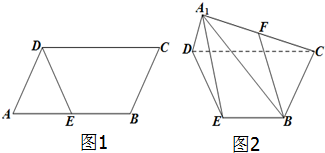 已知平行四边形ABCD(如图1),AB=4,AD=2,∠DAB=60°,E为AB的中点,把三角形ADE沿DE折起至A1DE位置,使得A1C=4,F是线段A1C的中点(如图2).
已知平行四边形ABCD(如图1),AB=4,AD=2,∠DAB=60°,E为AB的中点,把三角形ADE沿DE折起至A1DE位置,使得A1C=4,F是线段A1C的中点(如图2).