题目内容
19. 已知平行四边形ABCD(如图1),AB=4,AD=2,∠DAB=60°,E为AB的中点,把三角形ADE沿DE折起至A1DE位置,使得A1C=4,F是线段A1C的中点(如图2).
已知平行四边形ABCD(如图1),AB=4,AD=2,∠DAB=60°,E为AB的中点,把三角形ADE沿DE折起至A1DE位置,使得A1C=4,F是线段A1C的中点(如图2).(1)求证:BF∥面A1DE;
(2)求证:面A1DE⊥面DEBC;
(3)求二面角A1-DC-E的正切值.
分析 (1)取A1D中点G,并连接FG,EG,能够说明四边形BFGE为平行四边形,从而根据线面平行的判定定理即可得出BF∥面A1DE;
(2)先根据已知的边、角值说明△A1DE为等边三角形,然后取DE中点H,连接CH,从而得到A1H⊥DE,根据已知的边角值求出A1H,CH,得出${A}_{1}{H}^{2}+C{H}^{2}={A}_{1}{C}^{2}$,从而得到A1H⊥CH,从而根据线面垂直及面面垂直的判定定理即可证出面A1DE⊥面DEBC;
(3)过H作HO⊥DC,垂足为O,并连接A1O,容易说明DC⊥面A1HO,从而得出∠A1OH为二面角A1-DC-E的平面角,能够求出HO,从而求出tan∠A1OH,即求出了二面角A1-DC-E的正切值.
解答 解:(1)证明:如图,取DA1的中点G,连FG,GE; F为A1C中点;
F为A1C中点;
∴GF∥DC,且$GF=\frac{1}{2}DC=EB$;
∴四边形BFGE是平行四边形;
∴BF∥EG,EG?平面A1DE,BF?平面A1DE;
∴BF∥平面A1DE;
(2)证明:如图,取DE的中点H,连接A1H,CH;
AB=4,AD=2,∠DAB=60°,E为AB的中点;
∴△DAE为等边三角形,即折叠后△DA1E也为等边三角形;
∴A1H⊥DE,且${A}_{1}H=\sqrt{3}$;
在△DHC中,DH=1,DC=4,∠HDC=60°;
根据余弦定理,可得:
HC2=1+16-4=13,在△A1HC中,${A}_{1}H=\sqrt{3}$,$HC=\sqrt{13}$,A1C=4;
∴${A}_{1}{C}^{2}={A}_{1}{H}^{2}+H{C}^{2}$,即A1H⊥HC,DE∩HC=H;
∴A1H⊥面DEBC;
又A1H?面A1DE;
∴面A1DE⊥面DEBC;
(3)如上图,过H作HO⊥DC于O,连接A1O;
A1H⊥面DEBC;
∴A1H⊥DC,A1H∩HO=H;
∴DC⊥面A1HO;
∴DC⊥A1O,DC⊥HO;
∴∠A1OH是二面角A1-DC-E的平面角;
在Rt△A1HO中,${A}_{1}H=\sqrt{3}$,$HO=DH•sin60°=\frac{\sqrt{3}}{2}$;
故tan$∠{A}_{1}OH=\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}=2$;
所以二面角A1-DC-E的正切值为2.
点评 考查中位线的性质,平行四边形的概念,线面平行的判定定理,能根据折叠前图形的边角值得到折叠后对应的边角值,直角三角形边的关系,线面垂直、面面垂直的判定定理,二面角的平面角的定义及求法.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案| A. | $\frac{32}{3}$,-6 | B. | $\frac{32}{3}$,0 | C. | 6,-$\frac{32}{3}$ | D. | 6,0 |
 如图,焦点在x轴上的椭圆C1和焦点在y轴上的椭圆C2相切于点(0,2)、(0,-2),且椭圆C1,C2的离心率均为$\frac{\sqrt{3}}{2}$.
如图,焦点在x轴上的椭圆C1和焦点在y轴上的椭圆C2相切于点(0,2)、(0,-2),且椭圆C1,C2的离心率均为$\frac{\sqrt{3}}{2}$. 一张长方形纸片ABCD,AB=8cm,AD=6cm,将纸片沿着一条直线折叠,折痕(线段MN)将纸片分成两部分,面积分别为S1 cm2,S2 cm2,(S1≤S2)其中点A在面积为S1的部分内.记折痕长为lcm.
一张长方形纸片ABCD,AB=8cm,AD=6cm,将纸片沿着一条直线折叠,折痕(线段MN)将纸片分成两部分,面积分别为S1 cm2,S2 cm2,(S1≤S2)其中点A在面积为S1的部分内.记折痕长为lcm. 如图四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,G为MC中点,则下列结论中正确的是①②④.
如图四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,G为MC中点,则下列结论中正确的是①②④.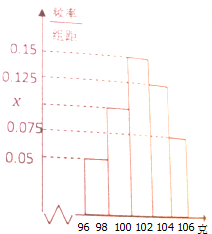 某工厂从一批产品中随机抽取40件进行检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).
某工厂从一批产品中随机抽取40件进行检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).