题目内容
16.已知函数f(x)=sin(2ωx-$\frac{π}{6}$)+2cos2ωx-1(ω>0),直线x=x1,x=x2是y=f(x)图象的任意两条对称轴,且|x1-x2|的最小值为$\frac{π}{2}$.(1)求ω的值;
(2)求函数f(x)在区间[-$\frac{π}{6}$,$\frac{π}{2}$]上的值域;
(3)若f(a)=$\frac{1}{3}$,求sin($\frac{7π}{6}$-4a)的值.
分析 (1)由题意,先化简f(x)=sin(2ωx-$\frac{π}{6}$)+2cos2ωx-1,得到f(x)=sin(2ωx+$\frac{π}{6}$),再直线x=x1,x=x2是y=f(x)图象的任意两条对称轴,且|x1-x2|的最小值为$\frac{π}{2}$,得出周期,由周期公式求出ω的值;
(2)求出-$\frac{π}{6}$≤2x+$\frac{π}{6}$≤$\frac{7π}{6}$,借助正弦函数求出-$\frac{1}{2}$≤f(x)≤1.
(3)由f(x)=sin(2x+$\frac{π}{6}$)
得f(a)=sin(2a+$\frac{π}{6}$)=$\frac{1}{3}$,再由诱导公式及二倍角公式化简sin($\frac{7π}{6}$-4a)=
2sin2(2a+$\frac{π}{6}$)-1,然后代入数据即可.
解答 解:(1)f(x)=sin(2ωx-$\frac{π}{6}$)+2cos2ωx-1=$\frac{\sqrt{3}}{2}$sin2ωx-$\frac{1}{2}$cos2ωx+cos2ωx=$\frac{\sqrt{3}}{2}$sin2ωx+$\frac{1}{2}$cos2ωx=sin(2ωx+$\frac{π}{6}$)
又直线x=x1,x=x2是y=f(x)图象的任意两条对称轴,且|x1-x2|的最小值为$\frac{π}{2}$,可得周期T=π
又T=$\frac{2π}{2ω}$,即$\frac{2π}{2ω}$=π,解得ω=1
(2)∵x∈[-$\frac{π}{6}$,$\frac{π}{2}$],∴-$\frac{π}{6}$≤2x+$\frac{π}{6}$≤$\frac{7π}{6}$,∴-$\frac{1}{2}$≤f(x)≤1.
即函数f(x)在区间[-$\frac{π}{6}$,$\frac{π}{2}$]上的值域为[-$\frac{1}{2}$,1].
(3)∵f(x)=sin(2x+$\frac{π}{6}$)
∴f(a)=sin(2a+$\frac{π}{6}$)=$\frac{1}{3}$
∴sin($\frac{7π}{6}$-4a)=sin(4a-$\frac{π}{6}$)=sin(4a+$\frac{π}{3}$-$\frac{π}{2}$)=-cos(4a+$\frac{π}{3}$)=2sin2(2a+$\frac{π}{6}$)-1=2×$\frac{1}{9}$-1=-$\frac{7}{9}$.
点评 本题考查三角恒等变换的应用及三角函数的最值,解三角方程,周期公式,熟练掌握三角函数的性质及变换公式是解题的关键.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案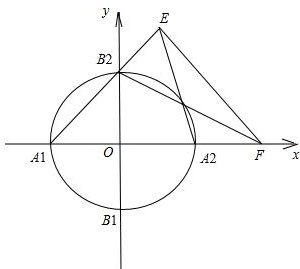 设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,直线y=x+$\sqrt{2}$与以原点为圆心、椭圆C的短半轴长为半径的圆O相切.
设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,直线y=x+$\sqrt{2}$与以原点为圆心、椭圆C的短半轴长为半径的圆O相切.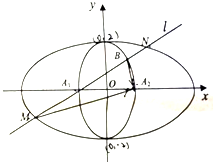 如图,焦点在x轴上的椭圆C1和焦点在y轴上的椭圆C2相切于点(0,2)、(0,-2),且椭圆C1,C2的离心率均为$\frac{\sqrt{3}}{2}$.
如图,焦点在x轴上的椭圆C1和焦点在y轴上的椭圆C2相切于点(0,2)、(0,-2),且椭圆C1,C2的离心率均为$\frac{\sqrt{3}}{2}$.