题目内容
12.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的下顶点为B(0,-1),B到焦点煌距离为2.(1)设Q是椭圆上的动点,求|BQ|的最大值;
(2)直线l过定点P(0,2)与椭圆C交于两点M,N,△BMN的面积为$\frac{6}{5}$,求直线l的方程.
分析 (1)由已知可得椭圆方程,设出动点Q的坐标,写出BQ的距离,结合动点Q在椭圆上转化为关于Q纵坐标的函数式,然后利用配方法求得最大值;
(2)设出直线l的方程,和椭圆方程联立,由判别式大于0求出k的范围,利用根与系数关系得到M,N的横坐标的和与积,由弦长公式求得弦长,再由点到直线的距离公式求出B到直线l的距离,代入三角形的面积公式求k.
解答 解:(1)由题意可知,b=1,a=2,
∴椭圆方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$.
设Q(x0,y0)(-1≤y0≤1),则$\frac{{{x}_{0}}^{2}}{4}+{{y}_{0}}^{2}=1$,
∴${{x}_{0}}^{2}=4-4{{y}_{0}}^{2}$.
∴$|BQ|=\sqrt{{{x}_{0}}^{2}+({y}_{0}+1)^{2}}$=$\sqrt{4-4{{y}_{0}}^{2}+{{y}_{0}}^{2}+2{y}_{0}+1}$
=$\sqrt{-3({y}_{0}-\frac{1}{3})^{2}+\frac{16}{3}}$.
∴当${y}_{0}=\frac{1}{3}$时,|BQ|有最大值为$\frac{4\sqrt{3}}{3}$;
(2)由题意可知,直线l的斜率存在且不为0,
设直线l的方程为y=kx+2.
联立$\left\{\begin{array}{l}{y=kx+2}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,消去y并化简得:(1+4k2)x2+16kx+12=0.
由△=(16k)2-48(1+4k2)=64k2-48>0,解得:$k<-\frac{\sqrt{3}}{2}$或k$>\frac{\sqrt{3}}{2}$.
${x}_{1}+{x}_{2}=-\frac{16k}{1+4{k}^{2}},{x}_{1}{x}_{2}=\frac{12}{1+4{k}^{2}}$.
|MN|=$\sqrt{1+{k}^{2}}•|{x}_{1}-{x}_{2}|$=$\sqrt{1+{k}^{2}}\sqrt{(-\frac{16k}{1+4{k}^{2}})^{2}-4•\frac{12}{1+4{k}^{2}}}$=$4\sqrt{1+{k}^{2}}•\frac{\sqrt{4{k}^{2}-3}}{1+4{k}^{2}}$.
B(0,-1)到直线y=kx+2的距离d=$\frac{3}{\sqrt{1+{k}^{2}}}$.
∴${S}_{△MNB}=\frac{1}{2}•4\sqrt{1+{k}^{2}}•\frac{\sqrt{4{k}^{2}-3}}{1+4{k}^{2}}•\frac{3}{\sqrt{1+{k}^{2}}}$=$\frac{6\sqrt{4{k}^{2}-3}}{1+4{k}^{2}}=\frac{6}{5}$.
解得:k2=1或${k}^{2}=\frac{19}{4}$.
∴k=±1或k=$±\frac{\sqrt{19}}{2}$.符合$k<-\frac{\sqrt{3}}{2}$或k$>\frac{\sqrt{3}}{2}$.
则所求的直线方程为y=-x+2,y=x+2,y=-$\frac{\sqrt{19}}{2}$x+2,y=$\frac{\sqrt{19}}{2}x+2$.
点评 本题考查由椭圆的几何性质求其方程,考查了直线和圆锥曲线的位置关系,涉及直线和圆锥曲线的位置关系问题,常采用联立直线和圆锥曲线方程,然后借助于一元二次方程根与系数关系求解,特点是运算量大,要求考生具有较强的运算能力,是压轴题.

| A. | $\frac{32}{3}$,-6 | B. | $\frac{32}{3}$,0 | C. | 6,-$\frac{32}{3}$ | D. | 6,0 |
 设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,直线y=x+$\sqrt{2}$与以原点为圆心、椭圆C的短半轴长为半径的圆O相切.
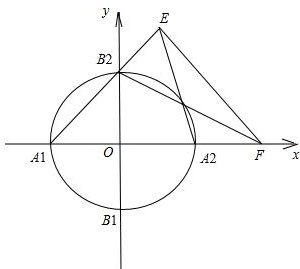
设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,直线y=x+$\sqrt{2}$与以原点为圆心、椭圆C的短半轴长为半径的圆O相切.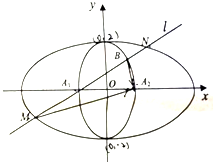 如图,焦点在x轴上的椭圆C1和焦点在y轴上的椭圆C2相切于点(0,2)、(0,-2),且椭圆C1,C2的离心率均为$\frac{\sqrt{3}}{2}$.
如图,焦点在x轴上的椭圆C1和焦点在y轴上的椭圆C2相切于点(0,2)、(0,-2),且椭圆C1,C2的离心率均为$\frac{\sqrt{3}}{2}$.