题目内容
10.写出满足下列条件的x的取值范围:(1)tanx>0;
(2)tanx=0;
(3)tanx<0.
分析 由条件结合正切函数的图象,可得结论.
解答 解:由函数y=tanx的图象可得,(1)当x∈(kπ,kπ+$\frac{π}{2}$),k∈z 时,tanx>0;
(2)当x=kπ,k∈z 时,tanx=0;
(3)当x∈(kπ-$\frac{π}{2}$,kπ),k∈z 时,tanx<0.
点评 本题主要考查正切函数的图象特征,属于基础题.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
2.函数f(x)=$\frac{2}{3}$x3-8x在区间[-3,0]上的最大值和最小值分别是( )
| A. | $\frac{32}{3}$,-6 | B. | $\frac{32}{3}$,0 | C. | 6,-$\frac{32}{3}$ | D. | 6,0 |
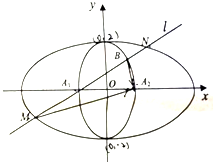 如图,焦点在x轴上的椭圆C1和焦点在y轴上的椭圆C2相切于点(0,2)、(0,-2),且椭圆C1,C2的离心率均为$\frac{\sqrt{3}}{2}$.
如图,焦点在x轴上的椭圆C1和焦点在y轴上的椭圆C2相切于点(0,2)、(0,-2),且椭圆C1,C2的离心率均为$\frac{\sqrt{3}}{2}$. 一张长方形纸片ABCD,AB=8cm,AD=6cm,将纸片沿着一条直线折叠,折痕(线段MN)将纸片分成两部分,面积分别为S1 cm2,S2 cm2,(S1≤S2)其中点A在面积为S1的部分内.记折痕长为lcm.
一张长方形纸片ABCD,AB=8cm,AD=6cm,将纸片沿着一条直线折叠,折痕(线段MN)将纸片分成两部分,面积分别为S1 cm2,S2 cm2,(S1≤S2)其中点A在面积为S1的部分内.记折痕长为lcm.