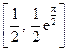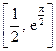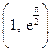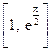题目内容
(2013•浙江)已知a∈R,函数f(x)=2x3﹣3(a+1)x2+6ax
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若|a|>1,求f(x)在闭区间[0,|2a|]上的最小值.
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若|a|>1,求f(x)在闭区间[0,|2a|]上的最小值.
(1)y=6x﹣8
(2)f(x)在闭区间[0,|2a|]上的最小值为g(a)=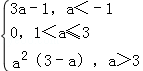 .
.
(2)f(x)在闭区间[0,|2a|]上的最小值为g(a)=
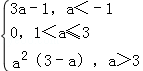 .
.(Ⅰ)当a=1时,f′(x)=6x2﹣12x+6,所以f′(2)=6
∵f(2)=4,∴曲线y=f(x)在点(2,f(2))处的切线方程为y=6x﹣8;
(Ⅱ)记g(a)为f(x)在闭区间[0,|2a|]上的最小值.
f′(x)=6x2﹣6(a+1)x+6a=6(x﹣1)(x﹣a)
令f′(x)=0,得到x1=1,x2=a
当a>1时,
比较f(0)=0和f(a)=a2(3﹣a)的大小可得g(a)=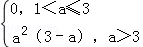 ;
;
当a<﹣1时,
∴g(a)=3a﹣1
∴f(x)在闭区间[0,|2a|]上的最小值为g(a)=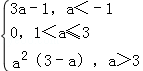 .
.
∵f(2)=4,∴曲线y=f(x)在点(2,f(2))处的切线方程为y=6x﹣8;
(Ⅱ)记g(a)为f(x)在闭区间[0,|2a|]上的最小值.
f′(x)=6x2﹣6(a+1)x+6a=6(x﹣1)(x﹣a)
令f′(x)=0,得到x1=1,x2=a
当a>1时,
| x | 0 | (0,1) | 1 | (1,a) | a | (a,2a) | 2a |
| f′(x) | | + | 0 | ﹣ | 0 | + | |
| f(x) | 0 | 单调递增 | 极大值3a﹣1 | 单调递减 | 极小值 a2(3﹣a) | 单调递增 | 4a3 |
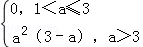 ;
;当a<﹣1时,
| X | 0 | (0,1) | 1 | (1,﹣2a) | ﹣2a |
| f′x) | | ﹣ | 0 | + | |
| f(x) | 0 | 单调递减 | 极小值3a﹣1 | 单调递增 | ﹣28a3﹣24a2 |
∴f(x)在闭区间[0,|2a|]上的最小值为g(a)=
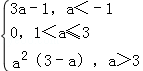 .
.
练习册系列答案
相关题目
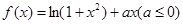
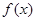 的单调性.
的单调性.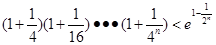 (
(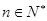 ,e为自然对数的底数)
,e为自然对数的底数)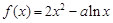 .
.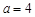 ,求函数
,求函数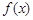 的极小值;
的极小值;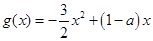 ,试问:在定义域内是否存在三个不同的自变量
,试问:在定义域内是否存在三个不同的自变量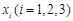 使得
使得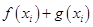 的值相等,若存在,请求出
的值相等,若存在,请求出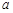 的范围,若不存在,请说明理由?
的范围,若不存在,请说明理由?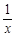 -(2+a)lnx(a≥0).
-(2+a)lnx(a≥0).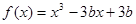 在
在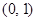 内有极小值,则
内有极小值,则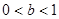
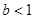
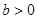

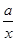 .
.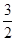 ,求实数a的值;
,求实数a的值; .
. 在
在 上为减函数,求实数
上为减函数,求实数 的最小值;
的最小值; ,使
,使 成立,求实数
成立,求实数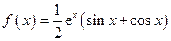 在区间
在区间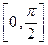 上的值域为( )
上的值域为( )