题目内容
已知函数f(x)=2ax-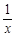 -(2+a)lnx(a≥0).
-(2+a)lnx(a≥0).
(1)当a=0时,求f(x)的极值;
(2)当a>0时,讨论f(x)的单调性;
(3)若对任意的a∈(2,3),x1,x2∈[1,3],恒有(m-ln3)a-2ln3>|f(x1)-f(x2)|成立,求实数m的取值范围。
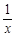 -(2+a)lnx(a≥0).
-(2+a)lnx(a≥0).(1)当a=0时,求f(x)的极值;
(2)当a>0时,讨论f(x)的单调性;
(3)若对任意的a∈(2,3),x1,x2∈[1,3],恒有(m-ln3)a-2ln3>|f(x1)-f(x2)|成立,求实数m的取值范围。
(1)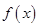 的极大值为
的极大值为 ,无极小值.(3)
,无极小值.(3)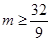
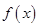 的极大值为
的极大值为 ,无极小值.(3)
,无极小值.(3)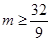
试题分析:(1)求已知函数的极值,利用导数法,即求定义域,求导,求导数为0与单调区间,判断极值点求出极值. (2) 求定义域,求导.利用数形结合思想讨论导数(含参数二次不等式)的符号求f(x)的单调区间,讨论二次含参数不等式注意按照定性(二次项系数是否为0),开口,判别式,两根大小得顺序依次进行讨论,进而得到函数f(x)的单调性(注意单调区间为定义域的子集)(3)这是一个恒成立问题,只需要(m-ln3)a-2ln3>(|f(x1)-f(x2)|)
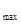 ,故求解确定|f(x1)-f(x2)|最大值很关键,分析可以发现(|f(x1)-f(x2)|)
,故求解确定|f(x1)-f(x2)|最大值很关键,分析可以发现(|f(x1)-f(x2)|)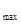 =
=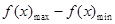 ,故可以利用第二问单调性来求得函数的最值进而得到(|f(x1)-f(x2)|)
,故可以利用第二问单调性来求得函数的最值进而得到(|f(x1)-f(x2)|)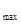 . (m-ln3)a-2ln3>(|f(x1)-f(x2)|)
. (m-ln3)a-2ln3>(|f(x1)-f(x2)|)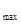 对于任意的a∈(2, 3)恒成立,则也是一个恒成立问题,可以采用分离参数法就可以求的m的取值范围.
对于任意的a∈(2, 3)恒成立,则也是一个恒成立问题,可以采用分离参数法就可以求的m的取值范围.试题解析:(1)当
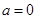 时,
时,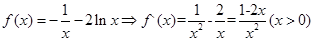 ,由
,由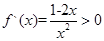 ,解得
,解得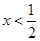 ,可知
,可知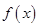 在
在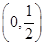 上是增函数,在
上是增函数,在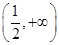 上是减函数.
上是减函数. ∴
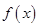 的极大值为
的极大值为 ,无极小值.
,无极小值.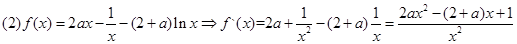
①当
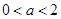 时,
时,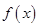 在
在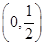 和
和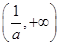 上是增函数,在
上是增函数,在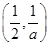 上是减函数;
上是减函数;②当
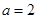 时,
时,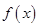 在
在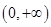 上是增函数;
上是增函数;③当
 时,
时,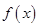 在
在 和
和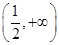 上是增函数,在
上是增函数,在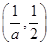 上是减函数 8分
上是减函数 8分(3)当
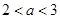 时,由(2)可知
时,由(2)可知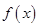 在
在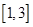 上是增函数,
上是增函数,∴
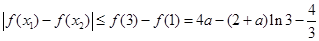 .
. 由
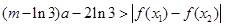 对任意的a∈(2, 3),x1, x2∈[1, 3]恒成立,
对任意的a∈(2, 3),x1, x2∈[1, 3]恒成立,∴
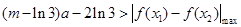
即
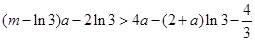 对任意
对任意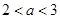 恒成立,
恒成立,即
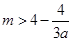 对任意
对任意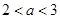 恒成立,由于当
恒成立,由于当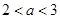 时,
时,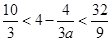 ,∴
,∴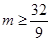 .
. 
练习册系列答案
相关题目
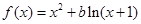 ,其中b≠0.
,其中b≠0.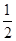 时,判断函数
时,判断函数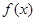 在定义域上的单调性:
在定义域上的单调性: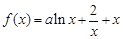 ,其中
,其中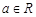 .
.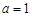 ,求函数
,求函数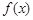 的极值点;
的极值点;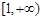 内单调递增,求实数
内单调递增,求实数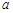 的取值范围.
的取值范围.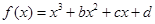 在区间
在区间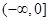 和
和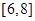 上单调递增,在
上单调递增,在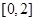 上单调递减,其图象与
上单调递减,其图象与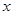 轴交于
轴交于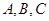 三点,其中点
三点,其中点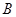 的坐标为
的坐标为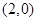 .
.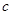 的值;
的值;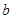 的取值范围;
的取值范围;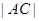 的取值范围.
的取值范围.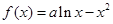 .
.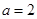 时,求函数
时,求函数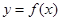 在
在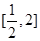 上的最大值;
上的最大值;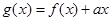 ,若
,若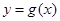 在区间
在区间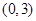 上不单调,求
上不单调,求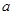 的取值范围;
的取值范围;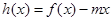 的图像与x轴交于两点
的图像与x轴交于两点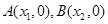 ,且
,且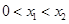 ,又
,又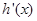 是
是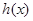 的导函数,若正常数
的导函数,若正常数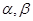 满足条件
满足条件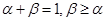 .证明:
.证明: .
. 的最大值是( )
的最大值是( )



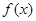 在区间
在区间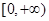 上满足
上满足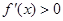 ,则满足
,则满足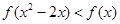 的
的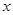 的取值范围是
的取值范围是


