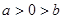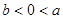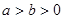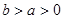题目内容
已知函数f(x)=ln x-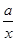 .
.
(1)当a>0时,判断f(x)在定义域上的单调性;
(2)f(x)在[1,e]上的最小值为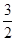 ,求实数a的值;
,求实数a的值;
(3)试求实数a的取值范围,使得在区间(1,+∞)上函数y=x2的图象恒在函数y=f(x)图象的上方.
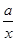 .
.(1)当a>0时,判断f(x)在定义域上的单调性;
(2)f(x)在[1,e]上的最小值为
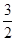 ,求实数a的值;
,求实数a的值;(3)试求实数a的取值范围,使得在区间(1,+∞)上函数y=x2的图象恒在函数y=f(x)图象的上方.
(1)f(x)在(0,+∞)上是单调递增函数
(2)a=-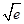 (3)a≥-1
(3)a≥-1
(2)a=-
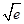 (3)a≥-1
(3)a≥-1(1)f′(x)=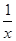 +
+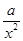 =
=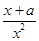 (x>0),
(x>0),
当a>0时,f′(x)>0恒成立,
故f(x)在(0,+∞)上是单调递增函数.
(2)由f′(x)=0得x=-a,
①当a≥-1时,f′(x)≥0在[1,e]上恒成立,f(x)在[1,e]上为增函数.
f(x)min=f(1)=-a=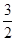 得a=-
得a=-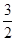 (舍).
(舍).
②当a≤-e时,f′(x)≤0在[1,e]上恒成立,f(x)在[1,e]上为减函数.
则f(x)min=f(e)=1- =
=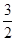 得a=-
得a=-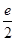 (舍).
(舍).
③当-e<a<-1时,由f′(x)=0得x0=-a.
当1<x<x0时,f′(x)<0,f(x)在(1,x0)上为减函数;
当x0<x<e时,f′(x)>0,f(x)在(x0,e)上为增函数.
∴f(x)min=f(-a)=ln(-a)+1=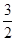 ,得a=-
,得a=-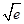 .
.
综上知:a=-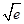 .
.
(3)由题意得:x2>ln x-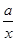 在(1,+∞)上恒成立,
在(1,+∞)上恒成立,
即a>xln x-x3在(1,+∞)上恒成立.
设g(x)=xln x-x3(x>1),则
g′(x)=ln x-3x2+1.
令h(x)=ln x-3x2+1,则
h′(x)=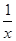 -6x.
-6x.
当x>1时,h′(x)<0恒成立.
∴h(x)=g′(x)=ln x-3x2+1在(1,+∞)上为减函数,
则g′(x)<g′(1)=-2<0.
所以g(x)在(1,+∞)上为减函数,
∴g(x)<g(1)<-1,故a≥-1
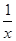 +
+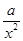 =
=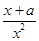 (x>0),
(x>0),当a>0时,f′(x)>0恒成立,
故f(x)在(0,+∞)上是单调递增函数.
(2)由f′(x)=0得x=-a,
①当a≥-1时,f′(x)≥0在[1,e]上恒成立,f(x)在[1,e]上为增函数.
f(x)min=f(1)=-a=
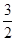 得a=-
得a=-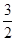 (舍).
(舍).②当a≤-e时,f′(x)≤0在[1,e]上恒成立,f(x)在[1,e]上为减函数.
则f(x)min=f(e)=1-
 =
=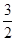 得a=-
得a=-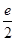 (舍).
(舍).③当-e<a<-1时,由f′(x)=0得x0=-a.
当1<x<x0时,f′(x)<0,f(x)在(1,x0)上为减函数;
当x0<x<e时,f′(x)>0,f(x)在(x0,e)上为增函数.
∴f(x)min=f(-a)=ln(-a)+1=
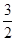 ,得a=-
,得a=-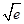 .
.综上知:a=-
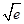 .
.(3)由题意得:x2>ln x-
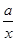 在(1,+∞)上恒成立,
在(1,+∞)上恒成立,即a>xln x-x3在(1,+∞)上恒成立.
设g(x)=xln x-x3(x>1),则
g′(x)=ln x-3x2+1.
令h(x)=ln x-3x2+1,则
h′(x)=
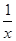 -6x.
-6x.当x>1时,h′(x)<0恒成立.
∴h(x)=g′(x)=ln x-3x2+1在(1,+∞)上为减函数,
则g′(x)<g′(1)=-2<0.
所以g(x)在(1,+∞)上为减函数,
∴g(x)<g(1)<-1,故a≥-1

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,其中
,其中 .
.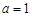 ,求函数
,求函数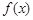 的极值点;
的极值点;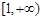 内单调递增,求实数
内单调递增,求实数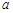 的取值范围.
的取值范围.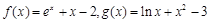 .若实数a, b满足
.若实数a, b满足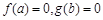 , 则 ( )
, 则 ( )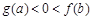
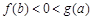
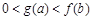
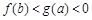
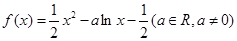 .
.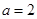 时,求曲线
时,求曲线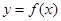 在点
在点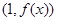 处的切线方程;
处的切线方程;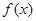 的单调区间;
的单调区间;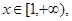 都有
都有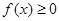 恒成立,求实数
恒成立,求实数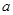 的取值范围.
的取值范围.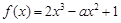 在区间
在区间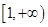 上为单调增函数,求
上为单调增函数,求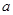 的取值范围.
的取值范围.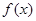 满足
满足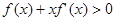 ,设
,设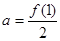 ,
,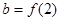 ,则
,则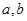 与
与 的大小关系为( )
的大小关系为( )