题目内容
设函数 .
.
(1)若函数 在
在 上为减函数,求实数
上为减函数,求实数 的最小值;
的最小值;
(2)若存在 ,使
,使 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 .
.(1)若函数
 在
在 上为减函数,求实数
上为减函数,求实数 的最小值;
的最小值;(2)若存在
 ,使
,使 成立,求实数
成立,求实数 的取值范围.
的取值范围.(1)a的最小值为 ;(2)
;(2)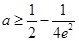 .
.
 ;(2)
;(2)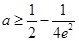 .
.试题分析:(1)根据f (x)在
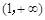 上为减函数,得到
上为减函数,得到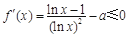 在
在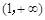 上恒成立.转化成
上恒成立.转化成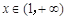 时,
时,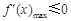 .
.应用导数确定其最大值为
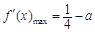 .
.(2)应用“转化与化归思想”,对命题进行一系列的转化,“若存在
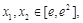 使
使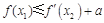 成立”等价于“当
成立”等价于“当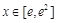 时,有
时,有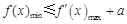 ”.
”.由(1)问题等价于:“当
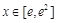 时,有
时,有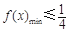 ”.
”.讨论①当
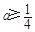 时,②当
时,②当 <
<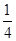 时,
时,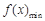 ,作出结论.
,作出结论.(1)由已知得x>0,x≠1.
因f (x)在
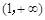 上为减函数,故
上为减函数,故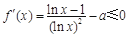 在
在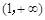 上恒成立. 1分
上恒成立. 1分所以当
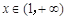 时,
时,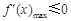 .
.又
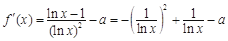
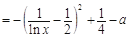 , 2分
, 2分故当
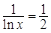 ,即
,即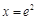 时,
时,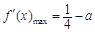 .
.所以
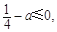 于是
于是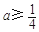 ,故a的最小值为
,故a的最小值为 . 4分
. 4分(2)命题“若存在
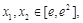 使
使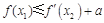 成立”等价于
成立”等价于“当
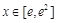 时,有
时,有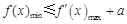 ”. 5分
”. 5分由(1),当
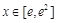 时,
时,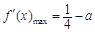 ,
,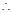
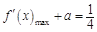 .
.问题等价于:“当
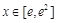 时,有
时,有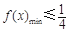 ”. 6分
”. 6分①当
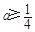 时,由(1),
时,由(1),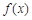 在
在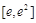 上为减函数,
上为减函数,则
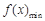 =
=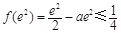 ,故
,故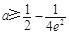 . 8分
. 8分②当
 <
<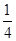 时,由于
时,由于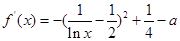 在
在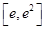 上的值域为
上的值域为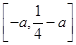
(ⅰ)
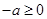 ,即
,即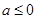 ,
,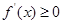 在
在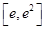 恒成立,故
恒成立,故 在
在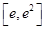 上为增函数,
上为增函数,于是,
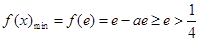 ,矛盾. 10分
,矛盾. 10分(ⅱ)
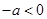 ,即
,即 ,由
,由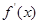 的单调性和值域知,
的单调性和值域知,存在唯一
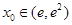 ,使
,使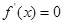 ,且满足:
,且满足:当
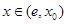 时,
时, ,
, 为减函数;当
为减函数;当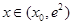 时,
时,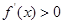 ,
, 为增函数;
为增函数;所以,
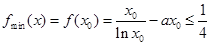 ,
,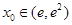 12分
12分所以,
 ,与
,与 矛盾. 13分
矛盾. 13分综上,得
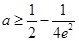 14分
14分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
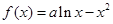 .
.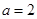 时,求函数
时,求函数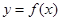 在
在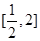 上的最大值;
上的最大值;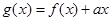 ,若
,若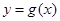 在区间
在区间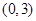 上不单调,求
上不单调,求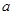 的取值范围;
的取值范围;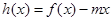 的图像与x轴交于两点
的图像与x轴交于两点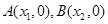 ,且
,且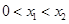 ,又
,又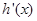 是
是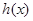 的导函数,若正常数
的导函数,若正常数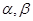 满足条件
满足条件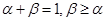 .证明:
.证明: .
.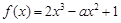 在区间
在区间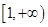 上为单调增函数,求
上为单调增函数,求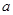 的取值范围.
的取值范围. ]
]