题目内容
(本题满分14分)
如图,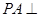 平面
平面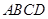 ,四边形
,四边形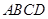 是矩形,
是矩形,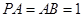 ,
,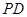 与平面
与平面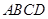 所成角是
所成角是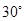 ,点
,点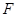 是
是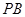 的中点,点
的中点,点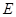 在矩形
在矩形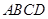 的边
的边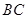 上移动.
上移动.
(1)证明:无论点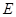 在边
在边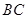 的何处,都有
的何处,都有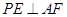 ;
;
(2)当 等于何值时,二面角
等于何值时,二面角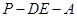 的大小为
的大小为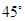 .
.
如图,
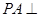 平面
平面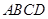 ,四边形
,四边形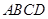 是矩形,
是矩形,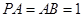 ,
,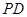 与平面
与平面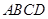 所成角是
所成角是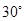 ,点
,点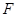 是
是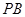 的中点,点
的中点,点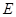 在矩形
在矩形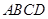 的边
的边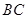 上移动.
上移动.(1)证明:无论点
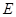 在边
在边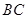 的何处,都有
的何处,都有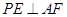 ;
;(2)当
 等于何值时,二面角
等于何值时,二面角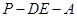 的大小为
的大小为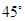 .
.
解:法一:(1)证明: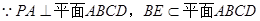 ,
,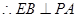 .
.

又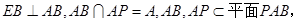
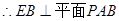 ,
,
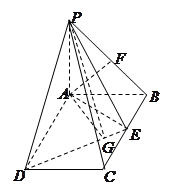
又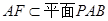 ,∴
,∴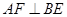
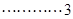 分
分
又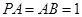 ,点
,点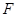 是
是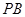 的中点,
的中点,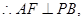
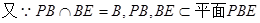 ,
, .
.
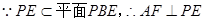 .
.  分
分
(2)过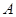 作
作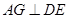 于
于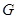 ,连
,连 ,又∵
,又∵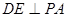 ,
,
则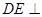 平面
平面 ,
,
则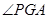 是二面角
是二面角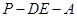 的平面角,
的平面角,
∴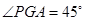 -------------------------------------------------------------------------- 9分
-------------------------------------------------------------------------- 9分
∵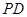 与平面
与平面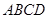 所成角是
所成角是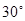 ,∴
,∴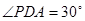 ,-------------------------------- 10分
,-------------------------------- 10分
∴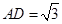 ,
,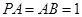 . ∴
. ∴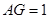 ,
,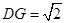 , -------------------------- 11分
, -------------------------- 11分
设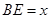 ,则
,则 ,
,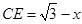 ,
,
在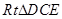 中,
中, ,
,
得 .故
.故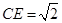 。 ------------------ 14分
。 ------------------ 14分
法二:(1)建立如图所示空间直角坐标系,则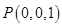 ,
,
∵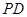 与平面
与平面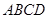 所成角是
所成角是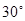 ,∴
,∴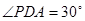 ,
,
∴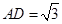 ,
,
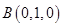 ,
,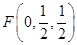 ,
, . ------ 3分
. ------ 3分
设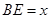 ,则
,则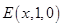
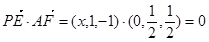
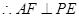 . --------------------------------6分
. --------------------------------6分
(2)设平面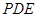 的法向量为
的法向量为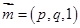 ,
,
由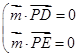 ,
,
得: , ---------------------------------------------- 8分
, ---------------------------------------------- 8分
而平面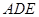 的法向量为
的法向量为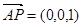 ,---------------------------------------------- 9分
,---------------------------------------------- 9分
∵二面角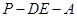 的大小是
的大小是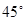 ,
,
所以 =
=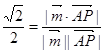 ,
,
∴ , ------------------- 11分
, ------------------- 11分
得 或
或 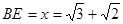 (舍).
(舍).
∴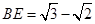 , 故
, 故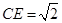 。 --------------------------------- 14分
。 --------------------------------- 14分
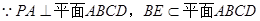 ,
,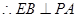 .
.
又
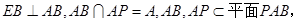
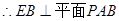 ,
,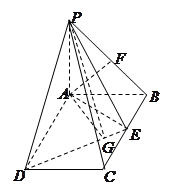
又
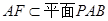 ,∴
,∴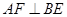
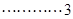 分
分又
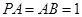 ,点
,点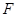 是
是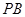 的中点,
的中点,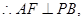
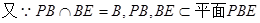 ,
, .
.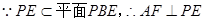 .
. 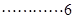 分
分(2)过
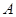 作
作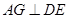 于
于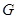 ,连
,连 ,又∵
,又∵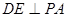 ,
,则
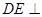 平面
平面 ,
,则
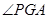 是二面角
是二面角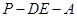 的平面角,
的平面角, ∴
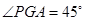 -------------------------------------------------------------------------- 9分
-------------------------------------------------------------------------- 9分∵
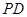 与平面
与平面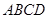 所成角是
所成角是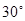 ,∴
,∴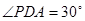 ,-------------------------------- 10分
,-------------------------------- 10分∴
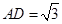 ,
,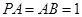 . ∴
. ∴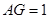 ,
,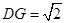 , -------------------------- 11分
, -------------------------- 11分设
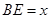 ,则
,则 ,
,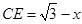 ,
,在
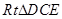 中,
中, ,
,得
 .故
.故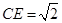 。 ------------------ 14分
。 ------------------ 14分法二:(1)建立如图所示空间直角坐标系,则
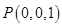 ,
, ∵
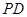 与平面
与平面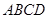 所成角是
所成角是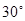 ,∴
,∴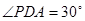 ,
,∴
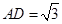 ,
,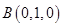 ,
,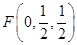 ,
, . ------ 3分
. ------ 3分设
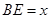 ,则
,则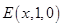
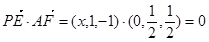
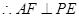 . --------------------------------6分
. --------------------------------6分(2)设平面
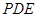 的法向量为
的法向量为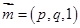 ,
,由
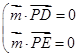 ,
,得:
 , ---------------------------------------------- 8分
, ---------------------------------------------- 8分而平面
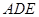 的法向量为
的法向量为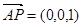 ,---------------------------------------------- 9分
,---------------------------------------------- 9分∵二面角
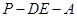 的大小是
的大小是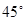 ,
,所以
 =
=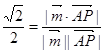 ,
,∴
 , ------------------- 11分
, ------------------- 11分得
 或
或 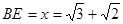 (舍).
(舍).∴
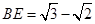 , 故
, 故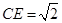 。 --------------------------------- 14分
。 --------------------------------- 14分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
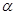 外”,正确的是( )
外”,正确的是( )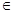 l, l
l, l 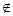
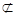
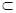 l, l
l, l 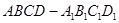 中,E、F分别是中点。
中,E、F分别是中点。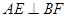 ;
;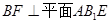 ;
;
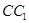 上是否存在点P使
上是否存在点P使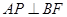 ,若存在,确定点P位置;若不存在,说明理由。
,若存在,确定点P位置;若不存在,说明理由。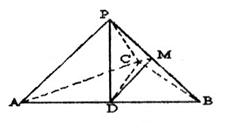
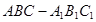 中,
中,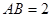 ,
,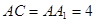 ,
,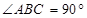 .
.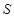 ;
;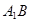 与
与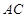 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).
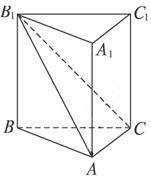
 中,
中,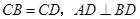 ,点
,点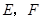 分别是
分别是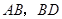 的中点. 求证:
的中点. 求证: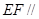 平面
平面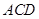 ;
;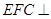 平面
平面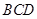 .
.
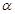 的一条斜线有一个平面与平面
的一条斜线有一个平面与平面